Основные определения и положения химической термодинамики. Взаимосвязь между основными законами, страница 18

Пусть моль идеального газа расширяется от объема V₁ до V₂. Примем, что молекулы имеют форму шара с объемом a.  Тогда количество ячеек , которые могут быть заняты  в том или ином объемах, равны соответственно V₁/а и  V₂./a. Термодинамические вероятности начального и конечного состояний будут равны: w₁= z(V₁/а)^N и w₂= z(V₁/а)^N. Поскольку S = k×lnw можно получить, что 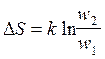, а также: 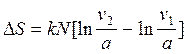  или после сокращения а имеем:

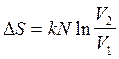                                                  (2.40)

Учитывая, что при расширении идеального газа T=const величина dU =0, в соответствии с уравнением dQ = dU + pdVимеем, что:

dQ = pdV                                                         (2.41)

Выразим давление через объем с помощью уравнения состояния идеального газа формулой p = RT/V. Подставим полученное выражение в уравнение (2.41) и получим 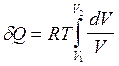. Отсюда:

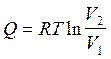                                                    (2.42)

Выразим из последнего уравнения логарифм отношения объемов и  подставим его в уравнение (2.40). Это приводит к следующему соотношению:

                                                   (2.43)

Больцман принял, что значение k соответствует равенству k=N/R. При этом условии, в конечном итоге имеем,  что:

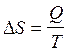.                                                 (2.44)

Полученное выражение является интегральной формой аналитического выражения второго закона термодинамики для обратимых процессов.

2.3.3. РАСЧЕТЫ ИЗМЕНЕНИЯ ЭНТРОПИИ

          ПРИ ХИМИЧЕСКИХ ПРОЦЕССАХ

Энтропия является функцией состояния системы. Поэтому ее изменение не зависит от пути протекания процесса и определяется только начальным и конечным состояниями системы. Нередко для случая идеального газа целесообразно воспользоваться свойством аддитивности энтропии, т.е. S_смеси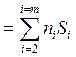

В основе многих расчетов изменения энтропии лежит соотношение:    

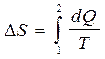                                                  (2.44 a)

Нередко полезными оказываются формулы для расчета энтропии, полученные в результате сочетания уравнения (2.44 a) с уравнениями  первого закона термодинамики. В частности с учетом уравнения (2.13) и закона Гей-Люссака выражение для первого закона термодинамики можно представить в следующем виде:

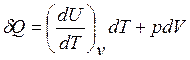                                            (2.45)

Сочетая уравнения (2.44) и (2.45) можно вывести, что:

dS = (C_v/T) dT +(p/T)dV                                      (2.46)

Интегрирование дает выражение для энтропии при условии, что независимыми переменными являются объем и температура, а n=1моль:

  или 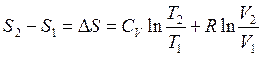                  (2.47)

Если процесс протекает при постоянной температуре уравнение (2.47) упростится к виду:

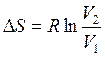                                                  (2.47 а)

В общем случае при расчетах изменения энтропии следует учитывать сумму всех возможных изменений энтропии на промежуточных стадиях.

Ниже представлены условия и результаты интегрирования уравнения (2.44) при конкретных условиях, отвечающих той или иной стадии процесса.

·  Адиабатический процесс (нет теплообмена): dQ =0; dS = 0.

·   Изотермический процесс. Фазовые превращения:

DS = S₂ -S_{1 =}                                (2.48)

где DН_фп  и Т_фп -соответственно энтальпия и температура фазового перехода.

·  Нагревание при постоянном давлении (изобарный процесс):

Поскольку, как следует из (2.29),  dQ =nC_pdT  с учетом (2.44) имеем:

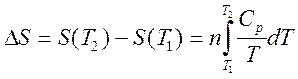                                    (2.49)

Если теплоемкость постоянна, то результатом интегрирования будет: DS=nC_p×ln(T₂/T₁)                                            (2.50)

·  Нагревание при постоянном объеме (изохорный процесс). Из (2.47) следует, что при dV=const:

                                        (2.51)

·  Пример соотношения для расчета изменения энтропии в процессе, включающем фазовый переход. при нагревании вещества при постоянном давлении

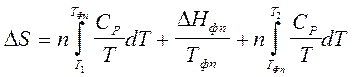                                 (2.52)  

Типовые примеры