Основные определения и положения химической термодинамики. Взаимосвязь между основными законами, страница 19

1.   Определите изменение энтропии при изотермическом увеличении объема 1 л азота до объема 2 л. При давлении и температуре равных соответственно 2 атм и 298 К.

Решение

Предположим, что газ идеальный. Это позволяет определить количество молей азота в заданной системе с помощью уравнения (1.3)  pV = nRT.                                         

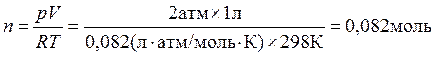
С учетом уравнения (2.47 а) 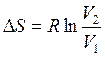  найдем DS:

DS = 0,082 моль×8,314(Дж/моль×К) ln 2 = 0,47  Дж/К

2. Вычислите изменение энтропии при испарении 1 моля воды при 100° С, если известно, что удельная  теплота испарения (DH_исп) при этой температуре  равна 2254,8∙10³  Дж/кг.

Решение

Испарение является обратимым изотермическим процессом, протекающим при постоянной температуре. Поэтому к нему можно применить следующее уравнение:    DS = S_г  -  S_ж = DH_исп/T_кип

С учетом того, что молярная теплота испарения равна DH_уд·18  имеем:

DS= 2254,8∙18/(273,2+100) = 108,77 Дж/моль∙К

2.4. ТРЕТИЙ ЗАКОН ТЕРМОДИНАМИКИ

Основные формулировки

Экспериментально в конце 19 века было показано, что при приближении к абсолютному нулю величина С_р стремится к 0, т.е.

lim С_р.= 0, если Т® 0  К.

Поэтому отношение С_р /Т  конечно или равно 0.  На основании этого положения с учетом уравнения (2.49) можно утверждать, что разность S_T - S_o всегда положительна или равна 0.

Из этого утверждения вытекают формулировки третьего закона термодинамики, в том числе:

·  Всякое вещество имеет конечную  положительную энтропию, которая при абсолютном нуле  может стать нулевой и действительно равна нулю в случае идеальной кристаллической решетки[23].

·  «Энтропия приобретает нулевое значение при любом давлении, коль скоро тело охлаждено до абсолютного нуля». Тепловая теорема Нернста в формулировке  К.А. Путилова [20].

Надо отметить, что выводы третьего закона термодинамики вполне согласуются с уравнением Больцмана  имеющего вид (2.9): S = k×lnw. Согласно этому уравнению для w.= 1 величина S = 0. Вместе с тем известно, что термодинамическая вероятность равна единице в одном случае, а именно, если макросостояние отвечает идеально правильно построенному кристаллу. Из этого заключения также вытекает и то, что газы, жидкости, аморфные фазы и растворы не должны подчиняться третьему закону термодинамики.

Расчеты абсолютного значения энтропии

Третий закон термодинамики предоставляет возможность рассчитывать абсолютную величину энтропии при любой температуре.

Действительно,  в соответствие с этим законом для идеального кристаллического вещества правомерно равенство: S_o=0. Поэтому из уравнения (2.51) следует,  что для моля вещества:

 S_T=C_p×ln(T_Т/T₀)                                                (2.53)

Величину C_pможно вычислить по формуле Дебая, применимой для расчетов вблизи абсолютного нуля:

C_p=a Т³                                                    (2.54)

Здесь a - экспериментально определяемая характеристика.

КОНТРОЛЬНОЕ ЗАДАНИЕ И ВОПРОСЫ

Выберите и обоснуйте правильное утверждение.

Энтропия кристаллического вещества по сравнению с тем же количеством паров этого вещества:

а) больше;

б) меньше;

в) одинакова.

При равновесном изотермическом сжатии энтропия некоторого количества идеального газа;

г) увеличится;

д) уменьшится;

е) не изменится.

2. В двух сообщающихся сосудах, разделенных перегородкой, находятся 1 моль N₂  и 2  моль О₂. Рассчитайте изменение энтропии смешения DS  после удаления перегородки, если исходные температуры и давления одинаковы, а объем V (N₂)  =1 л, объем V(O₂)= 2 л. Конечное давление равно исходному.

2. Определите DS для нагревания 1 моля азота при постоянном давлении от 300 до 1000 К, С_р =6,4492 + 1,4125×10^-3 T –0,807×10^-7 T².

3. Вычислите константу равновесия для реакции СO + 2Н₂=С Н₃OH_(г) при 750 K, если при 25^o С К_р=4,1∙10^-10 Па², а DH(750) =-103,5 кДж.

4. Вычислите изменение энтропии при испарении 1 моля хлористого этила при 12,3 ° С, если известно, что DH_исп = 376,83 кДж/кг.