Основные определения и положения химической термодинамики. Взаимосвязь между основными законами, страница 15

Теплоемкость идеального газа не зависит от температуры. Ее принимают равной 1,5 R для одноатомного газа и 2,5 R для двухатомного газа.

Интегрирование уравнения Кирхгофа

Для получения формулы, приемлемой для практических расчетов уравнение (2.31) надо проинтегрировать с учетом температурных зависимостей отдельных членов.

При интегрировании в узком диапазоне температур (несколько десятков градусов) теплоемкости отдельных веществ можно усреднить, считая их, а также величины  DC_pпостоянными. В этом случае имеем:

DH(T₂)- DH(T₁) = DC_p 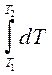                                              (2.35)

DH(T₂) =DH(T₁) + DC_p (T₂ -T₁)                                             (2.36)

Для оценки теплового эффекта при температуре (Т₂) необходимо знать величины теплоемкостей реагирующих веществ а также тепловой эффект реакции при некоторой начальной температуре (Т₁). Проблема снимается тем, что теплоемкости для большинства веществ приводятся в справочниках, а значение DH(T₁) можно посчитать для температуры 298 К, на основе закона Гесса,  пользуясь справочными данными для теплот образования реагирующих веществ (см. уравнение 2.24).

Типовые примеры

1.  Чему равно изменение энтальпии 1 моля воды при переходе из жидкого состояния при 20 °С в лед с температурой 0 °С (давление примите равным 101325 Па, теплоту плавления – 6 кДж/моль) и С_р = 75,5 Дж/моль×К?

Решение

Образование льда в рассмотренном случае проходит через две стадии: охлаждение воды и собственно кристаллизация. Поэтому изменение энтальпии следует представить алгебраической суммой

DH  = DH_т  + DH_фп

где:   DH_т  - изменение энтальпии при охлаждении системы до 0 °С; H_фп – изменение энтальпии при равновесном фазовом переходе.

Величину DH_т нетрудно определить из формулы DH_т = С_р(Т₂ – Т₁).  Она равна 1,51  кДж/моль, H_фп равна по абсолютной величине теплоте фазового перехода, т.е. 6 кДж/моль.

На обоих стадиях процесса система отдает энергию поэтому значения  DH_т  и DH_фп отрицательны и в сумме дают  – 7,51 кДж/моль.

2. Дана  реакция:  Н₂S _(г)  +3/2О_{2 (г)}   ® H₂О_(г)  + SO_2(г)

Найдите: 1) DH°  и DU°  при  25 С  2) DH° при 1000 °K

Решение.

а) Расчет DH° выполняем на основе уравнения (2.24) и справочных данных по теплотам образования реагентов из простых веществ (см. табл. 2.6).

DH°(298)= -241,84 – 296,9 –(-20,15) –0 = - 518,59 кДж

Для вычисления  DU° воспользуемся формулой (2.27):

DU°(298) = DH°(298) –RT (Dn)_г = -518,59 – 8,31×298×(-0,5) 10^-3 = -517,34 кДж

б) Расчет теплового эффекта при 1000 °K выполняем на основе  уравнений (2.34) и (2.36). Поскольку, по определению, теплоемкости представляют собой тепловые эффекты отнесенные к одному градусу, расчет величины DС_р можно выполнить на основе следствия из закона Гесса  (2.24). Это с учетом приведенных в таблице 2.6 данных по теплоемкостям приведет к следующему выражению для DС_р:

DС_р = - 0,52 +1,34×10^-3 Т – 1,46 ×10^-7 Т² + 0, 49×10^-9(Т³ кДж

Для DH°(1000) имеем в соответствии с правилами интегрирования:

DH°(1000) = DH°(298) +  -518,59 – 0,52 ×10^-3 (1000-298) +

+0,67×10^-6 (1000² -298²) – 0,49 ×10^-10(1000³ –298³) + 0,12×10^-12(1000⁴ –298⁴)  = -512,91 кДж

3. Рассчитайте работу расширения газа для реакции спиртового брожения глюкозы при 25^C:  

а) в закрытом сосуде; б) в открытом сосуде.

Решение

Протекает реакция  C₆H₁₂O₆ (aq)   =  2C₂H₅OН (aq) +  2CO₂ (газ) 

Образующийся газ производит работу - PDV . Принимая, что газ идеальный и пренебрегая начальным объемом системы, можно получить, что  PDV @PV(газ) @nRT.

Отсюда следует, что:

а) в закрытом сосуде

W = - PDV  = 0 (так как сосуд закрыт и газ не может расширяться);

б) в открытом сосуде

W = - PDV  = - n(СО₂)RT  = 2´8,31Дж/К·моль ´ 298 К = 4,953 кДж

КОНТРОЛЬНОЕ ЗАДАНИЕ И ВОПРОСЫ

Выберите и обоснуйте правильное утверждение.