Метод наименьших квадратов. Простая линейная регрессия

4.1. Метод наименьших квадратов

В дальнейшем мы будем рассматривать задачу аппроксимации только для одномерных переменных x = (x₀, x₁,…, x_n) и y = (y₀, y₁,…, y_n). Геометрически эта задача может быть сформулирована следующим образом: на плоскости OXY задано множество точек (x_i, y_i), 0 £ i £ n, требуется провести гладкую кривую, которая проходит достаточно близко от этих точек. Такую задачу также называют задачей простой регрессии. Задача простой регрессии заключается в построении функции g(x), связывающей переменные x = (x₀, x₁,…, x_n) и y = (y₀, y₁,…, y_n). При этом x считается независимой переменной, влияющей на значения переменной y. В дальнейшем будем полагать, что нам заданы некоторые экспериментальные данные (x_i, y_i), 0 £ i £ n, где n+1 – число измерений. Значения y_i могут быть заданы точно, а могут содержать погрешность, т.е.             y_i = f(x_i)+e_i, где f(x) – некоторая неизвестная функция, а e_i – погрешность. В простом регрессионном анализе, как правило, полагается, что e₀, e₁…e_n – независимые одинаково распределенные случайные величины.

Отметим, что любая аналитическая зависимость g = g(x), полученная в результате обработки данных, называется эмпирической формулой. Следует также отметить, что в отличии от задачи интерполяции, в этом случае не требуется, чтобы все узлы сетки были различны между собой. То есть данные могут содержать точки, имеющие одинаковые координаты по x (x_i = x_j  при i¹j).

Регрессионная функция (регрессионная модель, модель регрессии, эмпирическая формула) g = g(x) считается функцией, зависящей от параметров c₁, c₂,…, c_k, где k<n+1, например, g(x) = c₁+c₂x. Таким образом, задача простой регрессии (задача аппроксимации, задача построения эмпирической формулы) разбивается на два этапа:

1)  выбор функции (модели) g = g(c₁, c₂, …, c_k, x);

2)  нахождение числовых значений параметров c₁, c₂, …, c_k.

Первый этап заметно сложнее второго. Предпочтение отдается простым формулам (полиномы, дробно-рациональные, показательные и другие функции). Нахождение параметров регрессионной функции (параметров регрессии, параметров регрессионной модели, параметров эмпирической формулы) является более легкой задачей, для решения которой используется метод наименьших квадратов (МНК), метод средних, метод выбранных точек и др. На практике чаще всего применяется метод наименьших квадратов, в дальнейшем мы будем использовать только этот метод.

Определение. Величины (y_i-g(c₁, c₂, …, c_k, x_i)) называются остатками.

Определение. Методом наименьших квадратов называется способ подбора параметров c₁, c₂, …, c_k регрессионной функции исходя из минимизации суммы квадратов остатков, т.е.:

.

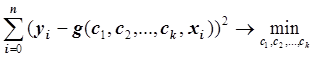Другими словами, метод наименьших квадратов – это метод нахождения параметров c = (c₁, c₂, …, c_k) для фиксированной регрессионной функции (регрессионной модели, эмпирической формулы) /3/, таких что функция

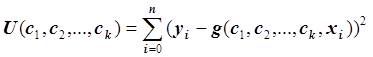
достигает минимума. Рассматривая функцию U как функцию от переменных c₁, c₂, …, c_k и используя необходимые условия экстремума функции нескольких переменных, получаем нормальную систему для определения параметров c₁, c₂, …, c_k:

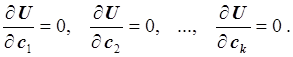
Если нормальная система имеет единственное решение, то это решение и будет искомым. Отметим, что если регрессионная функция g(c₁, c₂, …, c_k) является линейной функцией относительно c₁, c₂, …, c_k (например, ), то нормальная система является системой линейных уравнений с симметричной матрицей.

4.2. Простая линейная регрессия

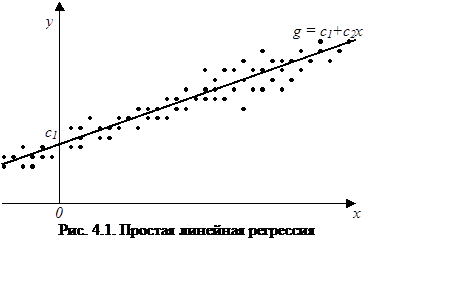Простая линейная регрессия заключается в нахождении функции                       g(c₁, c₂, x) = c₁+c₂x, описывающей связь между собой двух переменных x = (x₀, x₁,…, x_n) и y = (y₁, y₂,…, y_n). Таким образом, регрессионная функция уже выбрана, осталось определить параметры регрессии c₁ и c₂. Применим метод наименьших квадратов для их нахождения.

Требуется найти числа c₁ и c₂, доставляющие минимум функции

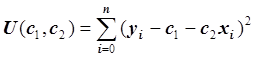
Геометрически эту задачу можно сформулировать следующим образом: в облаке точек на плоскости OXY требуется провести прямую, обеспечивая при этом наименьшую среднеквадратичную погрешность (рис. 4.1) /2/.

Функцию U(c₁, c₂) рассмотрим как функцию двух переменных - c₁ и c₂. Используя необходимые условия экстремума функции нескольких переменных, получаем нормальную систему:

,   .

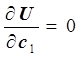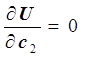Так как функция g = c₁+c₂x линейна относительно c₁ и c₂, то получаем систему линейных уравнений для нахождения неизвестных c₁ и c₂. Запишем первое уравнение:

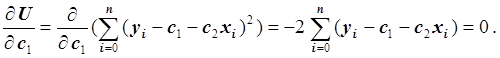
Умножив обе части уравнения на –0.5 и преобразовав, получим:

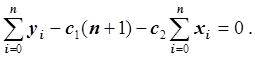
Запишем это уравнение в следующем виде: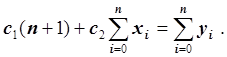  

Второе уравнение:

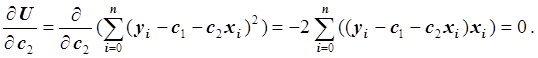
Умножив обе части на –0.5 и преобразовав, получим: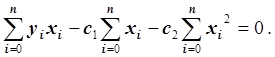  

Запишем уравнение в виде: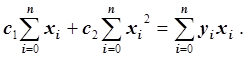  

Получаем систему линейных уравнений с симметрической матрицей:

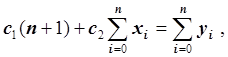
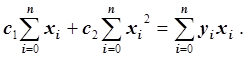
Таким образом, в случае простой линейной регрессии нормальная система является системой двух линейных уравнений с двумя неизвестными c₁ и c₂. Матрица этой системы линейных уравнений симметрична и невырожденна, следовательно, система линейных уравнений имеет единственное решение, которое ищется методом Гаусса с частичным выбором ведущего элемента. Таким образом, параметры простой линейной регрессии c₁ и c₂ определяются единственным образом.