Метод наименьших квадратов. Простая линейная регрессия, страница 12

ПРИМЕР ВЫПОЛНЕНИЯ ЗАДАНИЯ 1

Задание. Построить алгоритм для аппроксимации функции  на отрезке  регрессионной функцией  с использованием метода наименьших квадратов. Разработать программу, реализующую этот алгоритм. Размерность равномерной сетки равна 21.

Решение. Построение алгоритма в данном случае заключается в построении системы линейных уравнений и обоснования существования и единственности решения этой системы линейных уравнений. В дальнейшем будем опираться на материал, изложенный в п.п. 4.3.

Сначала построим сетку и таблицу данных. Так как сетка равномерная и число узлов сетки равно 21, то число отрезков  равно 20 (). Обозначим через  шаг, который вычисляется по формуле . В нашем случае , .

Введем сетку на отрезке : . Узлы сетки находятся по формуле ,  . Значение находится по формуле ,  . Таким образом, по формуле функции  на отрезке  построена таблица данных размерности 21 с равномерным шагом. Отметим, что в нашем случае эта таблица является интерполяционной таблицей, так как данные не содержат погрешностей.

Функцию  мы будем аппроксимировать функцией  методом наименьших квадратов. Следовательно, будем искать такие значения параметров ,  и , при которых функция достигает минимума, т.е.:

.

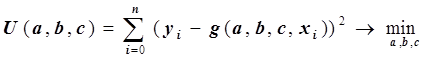Используя необходимые условия экстремума функции нескольких переменных, получаем нормальную систему для определения параметров ,  и :

,   ,   .

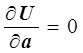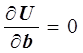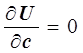Так как функция g является линейной функцией относительно ,  и , то получаем систему линейных уравнений. Запишем первое уравнение:

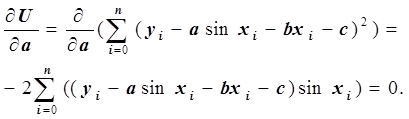
Умножив обе части уравнения на –0.5 и преобразовав, получим:

.

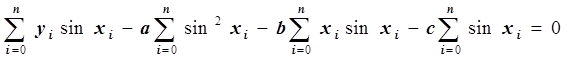Запишем это уравнение в виде:

.

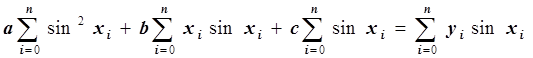Второе уравнение:

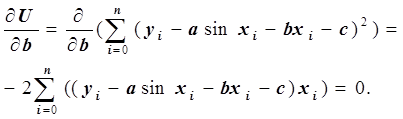
Умножив обе части уравнения на –0.5 и преобразовав, получим:

.

Запишем это уравнение в виде:

.

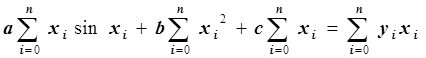Третье уравнение получаем аналогично:

.

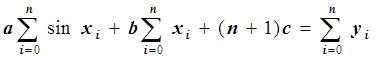Запишем систему линейных уравнений:

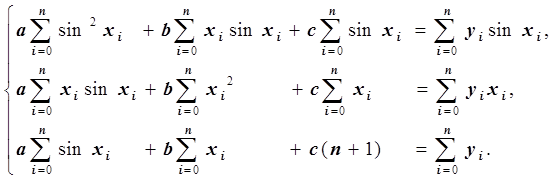
Мы получили систему линейных уравнений с симметричной матрицей. Эта матрица невырожденна, так как функции  линейно независимы. Следовательно, система линейных уравнений относительно неизвестных a, b и c имеет единственное решение, которое находится методом Гаусса с частичным выбором ведущего элемента.

Зная параметры ,  и , мы можем найти значение функции в любой точке отрезка . Значение среднеквадратичной погрешности находится по формуле 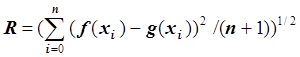. На печать выводится значение среднеквадратичной погрешности и таблица значений функций  и  в узлах сетки, т.е. значения ,   , ,   .

Отметим, что среднеквадратичная погрешность R может принимать достаточно большие значения. Связано это с тем, что эта погрешность является абсолютной погрешностью, а не относительной, а также с тем, что регрессионная функция может быть выбрана неудачно.

Программа

#include <stdio.h>

#include <math.h>

#include <conio.h>

// Функция f(x)

float fn (float x)

{ return (pow(2,x)-3*x+4); }

// Функция g(A ,B ,C, x)

float gx (float A,float B,float C,float x)

{ return (A*sin(x)+B*x+C); }

// Функция GaussMethod - решает СЛУ размерности 3

// Входные параметры: А - матрица, В - вектор, Х - вектор неизвестных

void GaussMethod(float A[3][3],float B[3],float X[3])

{

int    i,j; //счетчики циклов

// Решение системы уравнений

// k-счетчик циклов

// numb-номер строки с ведущим элементом

// max-максимальный по модулю элемент не преобразованного столбца

// str,bstr- используются при перестановке строк

// L-коэффициент преобразования

int    numb=0, k;

float max, str, bstr, L;

// Прямой ход метода Гаусса

for (j=0;j<2;j++)

{

max = fabs(A[j][j]);

numb = j;

      // определение максимального элемента в столбце

for (i=j;i<3;i++)

{

if (max<fabs(A[i][j]))

{ max=fabs(A[i][j]); numb=i; };

};

      // если максимум - не диагональный элемент, то...

if (numb!=j)

{

// ...замена строк

for (i=0;i<3;i++)

{

str = A[numb][i];

A[numb][i] = A[j][i];

A[j][i] = str;

};

bstr = B[numb];

B[numb] = B[j];

B[j] = bstr;

};

// преобразование столбца

for (i=j+1;i<3;i++)

{

L = -(A[i][j]/A[j][j]);  // вычисление коэффициента

A[i][j] = 0.0;

   // обнуление элемента текущего столбца

for (k  = j+1;k<3;k++) { A[i][k]=A[i][k]+A[j][k]*L; };

// и вычисление последующих в строке

B[i] = B[i]+B[j]*L;

};

};

// Обратная подстановка