Математика \ Вычислительная математика

Метод наименьших квадратов. Простая линейная регрессия, страница 5

Таким образом, от исходной задачи мы переходим к задаче нахождения параметров k и d таких, что функция 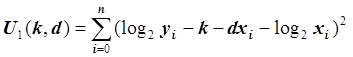достигает минимума. Рассматривая функцию U₁ как функцию переменных k и d и используя необходимые условия экстремума функции нескольких переменных, получаем нормальную систему:

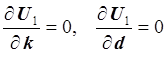Так как функция g₁(k, d, x) является линейной функцией относительно k и d, то получаем систему линейных уравнений для нахождения неизвестных k и d. Запишем первое уравнение:

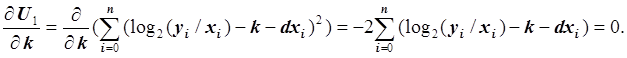
Умножив обе части уравнения на –0.5 и преобразовав, получим:

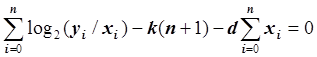Запишем это уравнение в виде: .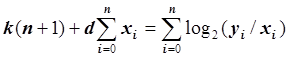

Второе уравнение:

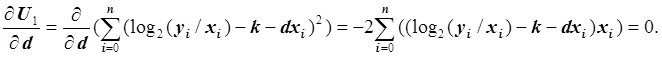
Умножив обе части уравнения на –0.5 и преобразовав, получим:

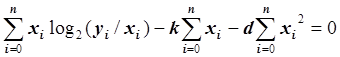Запишем это уравнение в виде:

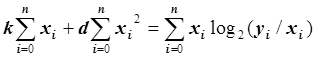Запишем систему линейных уравнений:

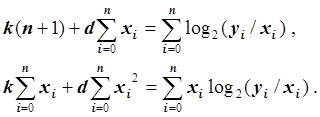
Мы получили систему линейных уравнений с симметричной невырожденной матрицей. Следовательно, система линейных уравнений относительно неизвестных k и d имеет единственное решение, которое находится методом Гаусса с частичным выбором ведущего элемента.

Укажем ограничения: x_i > 0, y_i > 0, 0 £ i £ n, c > 0. Зная параметры k и d, находим c = 2^k , теперь мы можем вычислить значение регрессионной функции g(c, d, x) для любого x из отрезка [x₀, x_n].

5. Временные ряды

Временной ряд – это числовая последовательность, характеризующая изменение явления во времени. Другими словами, временной ряд, ряд динамики, хронологический ряд, динамический ряд – это упорядоченная по времени последовательность числовых значений: y₁, y₂,…, y_n. Временной ряд включает последовательность значений времени t₁, t₂,…, t_n и последовательность измерений значений переменной в эти моменты времени: y₁, y₂,…, y_n. Значение y_i называют i-тым уровнем временного ряда. Таким образом, уровень временного ряда – это отдельное наблюдение временного ряда.

Многие явления в окружающем нас мире можно интерпретировать как временные ряды: изменение курса доллара, изменение цен и спроса на продукцию или сырьё, изменение уровня воды в реке и т.д.

Рекомендуемая литература: /3, 5, 6/.

5.1. Определения

Выделяют интервальные и моментные временные ряды. Интервальные временные ряды – это такие временные ряды, в которых каждый уровень характеризует величину изучаемого явления за соответствующий интервал времени. Например, объем выпущенной продукции по месяцам года, объем продаж по дням и т.д. В моментных временных рядах каждый уровень временного ряда отражает величину изучаемого явления на определенный момент времени. Например, численность населения на 01 января 2000 года, запас продовольствия на такое-то число и т.д. Отличие моментных рядов от интервальных заключается в том, что сумма уровней интервального ряда является некоторым реальным показателем – общий выпуск продукции за год, объем продаж за месяц, год и т.д. Сумма уровней моментного ряда реального содержания, как правило, не имеет /5/.

Пример. Временной ряд, составленный из значений курса доллара в определенные дни – это моментный временной ряд.

Часто рассматриваются временные ряды, в которых измерения производятся через равные моменты времени.

Для характеристики временных рядов вводятся следующие показатели: абсолютный прирост, коэффициент роста, темпы роста, коэффициент прироста, темп прироста. Когда i-тый уровень временного ряда y_i сравнивается с начальным уровнем ряда y₁, получаем базисные показатели. Если же y_i сравнивается с y_i_-1 (текущий уровень сравнивается с предыдущим), то получаем цепные показатели.

Абсолютный прирост D_i

(базисный), (цепной).