Метод наименьших квадратов. Простая линейная регрессия, страница 6

Всякий временной ряд теоретически может быть представлен в виде суммы составляющих y_i = f(t_i) + d_i + e_i, где f(t) – некоторая функция, называемая трендом,           d_i - циклические (периодические) колебания, в том числе сезонные, e_i – случайные отклонения. Сезонные колебания – это возрастание или убывание уровней ряда, повторяющиеся регулярно с определенным интервалом (например, потребление топлива и электроэнергии, сезонная продажа товаров и т.д.). В дальнейшем мы не будем рассматривать влияние сезонных колебаний, т.е. будем полагать, что y_i = f(t_i) + e_i. Полагаем, что e_i – независимые нормально распределенные случайные величины с нулевым математическим ожиданием (Me_i = 0) и дисперсией De_i = s_i² = s_i.

Одной из важных задач анализа временных рядов является выделение тренда, т.е. построение функции g(t), которая достаточно близка к f(t). Эту задачу называют задачей сглаживания.

Задача сглаживания. Задача сглаживания заключается в построении функции g(t), которая приближает неизвестный нам тренд f(t) на основании имеющегося у нас временного ряда (t_i, y_i), 1 £ i £ n.

Задача прогноза. По имеющимся значениям уровней временного ряда (t_i, y_i),        1 £ i £ n предсказать значения временного ряда (t_n+1, y_n+1), (t_n+2, y_n+2),…, (t_n+p, y_n+p).

Отметим, что при решении задачи прогноза сначала, как правило, решается задача сглаживания, а затем, используя тренд, строится прогноз. Функцию f(t) выбирают таким образом, чтобы она давала содержательное объяснение изучаемого процесса /5/.

5.3. Решение задач сглаживания и прогноза методом

наименьших квадратов

Для решения задач сглаживания и прогноза используются различные методы, мы рассмотрим только метод наименьших квадратов для линейной и параболической зависимостей.

Линейная зависимость

Линейная зависимость выбирается, как правило, в тех случаях, когда в исходном временном ряду более или менее постоянные абсолютные цепные приросты, не проявляющие тенденции ни к увеличению, ни к снижению /5/.

Пусть задан временной ряд (t_i, y_i), 1 £ i £ n. Считаем, что y_i = f(t_i)+e_i, 1 £ i £ n. Предполагаем, что тренд f(t) – линейная функция, а именно: f(t) = a+bt.

Применим метод наименьших квадратов для решения задачи сглаживания. Запишем функцию 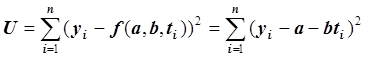 и будем искать такие значения параметров a и b, при которых функция U достигает минимума (см. п.п. 4.2). Запишем нормальную систему:

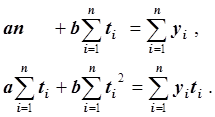
Эта система линейных уравнений имеет единственное решение, которое находится методом Гаусса с частичным выбором ведущего элемента. Функция f(t) = a+bt является решением задачи сглаживания.

Зная a и b, мы можем вычислить значение функции f(t) = a+bt  для любого значения t. Значения прогноза y_n+1, y_n+2,…, y_n+p, находятся по формуле y_n+j = f(a, b, t_n+j), где    j принимает значения 1, 2,…, p.

Параболическая (квадратичная) зависимость

Параболическая зависимость используется, если абсолютные цепные приросты обнаруживают некоторую тенденцию развития, но абсолютные цепные приросты абсолютных цепных приростов (разности второго порядка) никакой тенденции развития не проявляют /5/.

Пусть задан временной ряд (t_i, y_i), 1 £ i £ n. Считаем, что y_i = f(t_i)+e_i, 1 £ i £ n. Предполагаем, что тренд f(t) – параболическая (квадратичная) функция, а именно:    f(t) = a+bt+ct².

Применим метод наименьших квадратов для решения задачи сглаживания. Запишем функцию

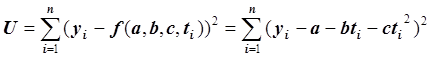
и будем искать такие значения параметров a, b и c, при которых функция U достигает минимума (см. п.п. 4.3). Запишем нормальную систему:

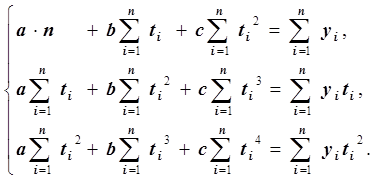
Эта система линейных уравнений имеет единственное решение, которое находится методом Гаусса с частичным выбором ведущего элемента. Функция f(t) = a+bt+ct² является решением задачи сглаживания.

Зная a, b и c, мы можем вычислить значение функции f(t) = a+bt+ct² для любого значения t. Значения прогноза y_n+1, y_n+2,…, y_n+p, находятся по формуле                         y_n+j = f(a, b, с, t_n+j), где   j принимает значения 1, 2,…, p.