Метод наименьших квадратов. Простая линейная регрессия, страница 4

Решение. Требуется построить алгоритм для нахождения параметров a и b регрессионной функции g(a, b, x) методом наименьших квадратов. Следовательно, будем искать такие значения параметров a и b, при которых функция 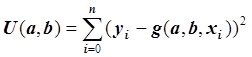 достигает минимума, т.е.:

.

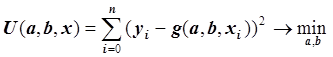Используя необходимые условия экстремума функции нескольких переменных (в данном случае двух переменных), получаем нормальную систему для определения параметров a и b:

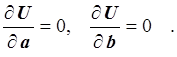
Так как функция g = g(a, b, x) является линейной функцией относительно a и b, то получаем систему линейных уравнений. Запишем первое уравнение:

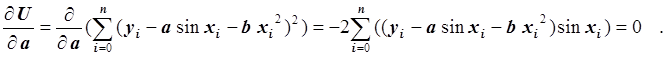
Умножив обе части уравнения на –0.5 и преобразовав, получим:

 .

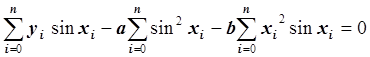Запишем это уравнение в виде:   .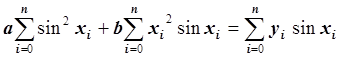

Второе уравнение:

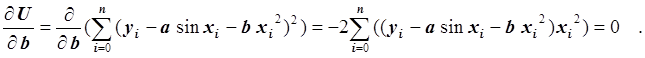
Умножив обе части уравнения на –0.5 и преобразовав, получим:

 .

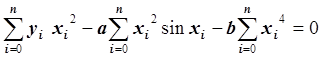Запишем это уравнение в виде:   .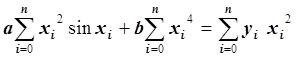

Запишем систему линейных уравнений:

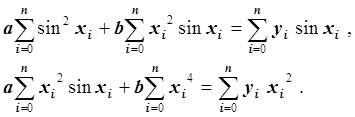
Мы получили систему линейных уравнений с симметричной матрицей. Эта матрица невырожденна, так как функции {sin x, x²} линейно независимы. Следовательно, система линейных уравнений относительно неизвестных a и b имеет единственное решение, которое находится методом Гаусса с частичным выбором ведущего элемента.

Зная параметры a и b, мы можем найти значение регрессионной функции g(a, b, x) для любого x из отрезка [x₀, x_n].

Задача 2. Пусть заданы экспериментальные данные (x_i, y_i), 0 £ i £ n. Используя метод наименьших квадратов, построить алгоритм для нахождения регрессионной функции g(a, b, c, x) = a cos x + be^x + cx, описывающей связь между x и y.

Решение. Требуется построить алгоритм для нахождения параметров a , b и c регрессионной функции g(a, b, с, x) методом наименьших квадратов. Следовательно, будем искать такие значения параметров a, b и c, при которых функция 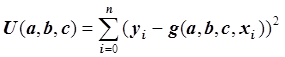 достигает минимума, т.е.:

.

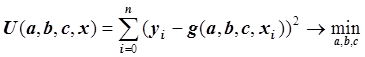Используя необходимые условия экстремума функции нескольких переменных (в данном случае трех переменных), получаем нормальную систему для определения параметров a , b и c:

.

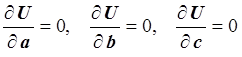Так как функция g = g(a, b, с, x) является линейной функцией относительно a , b и c, то получаем систему линейных уравнений. Запишем первое уравнение:

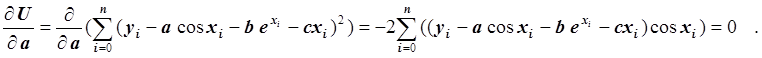
Умножив обе части уравнения на –0.5 и преобразовав, получим:

 .

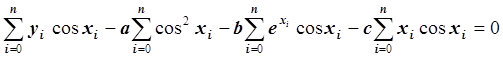Запишем это уравнение в виде: .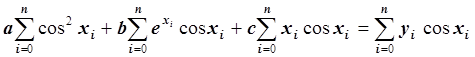

Второе уравнение:

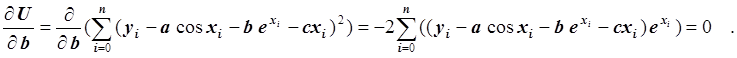
Умножив обе части уравнения на –0.5 и преобразовав, получим:

 .

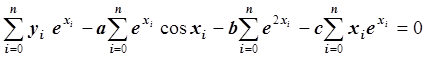Запишем это уравнение в виде:   .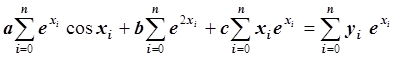

Третье уравнение:

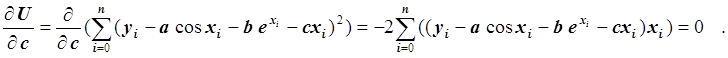
Умножив обе части уравнения на –0.5 и преобразовав, получим:

 .

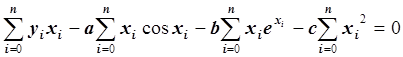Запишем это уравнение в виде:

.

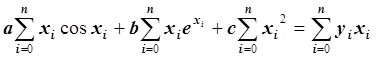Запишем систему линейных уравнений:

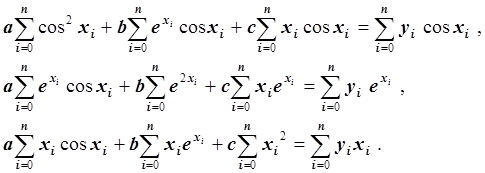
Мы получили систему линейных уравнений с симметричной матрицей. Эта матрица невырожденна, так как функции {cos x, e^x, x} линейно независимы. Следовательно, система линейных уравнений относительно неизвестных a, b и c имеет единственное решение, которое находится методом Гаусса с частичным выбором ведущего элемента.

Зная параметры a, b и c, мы можем найти значение регрессионной функции g(a, b, с, x) для любого x из отрезка [x₀, x_n].

Задача 3. Пусть заданы экспериментальные данные (x_i, y_i), 0 £ i £ n. Используя метод наименьших квадратов, построить алгоритм для нахождения регрессионной функции g(c, d, x) = с × x × 2^dx×, описывающей связь между x и y. Если необходимо, указать ограничения на x, y, c и d.

Решение. Требуется построить алгоритм для нахождения параметров c и d регрессионной функции g(c, d, x)  методом наименьших квадратов. Сначала применим линеаризующее преобразование F(z) = log₂ z. Получаем: g₁ = log₂ g = log₂ с + log₂ x + dx. Линеаризующее преобразование можно применить, если c > 0 и x_i > 0, 0 £ i £ n. Вводим новый параметр k = log₂ c и получаем функцию g₁, линейную относительно параметров k и d: g₁ = log₂ g = k + dx + log₂ x. Вместо функции 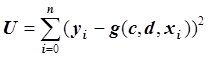 получаем функцию 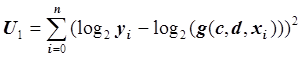. Для существования функции U₁ должны выполнятся условия: y_i > 0, 0 £ i £ n.