Метод наименьших квадратов. Простая линейная регрессия, страница 3

Таким образом, от исходной задачи мы переходим к задаче нахождения параметров k и d таких, что функция 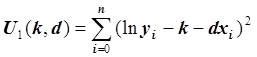достигает минимума. Рассматривая функцию U₁ как функцию переменных k и d и используя необходимые условия экстремума функции нескольких переменных, получаем нормальную систему:

.

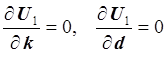Так как функция g₁(k, d, x) = k + dx является линейной функцией от k и d, то получаем систему линейных уравнений для нахождения неизвестных k и d. Запишем первое уравнение:

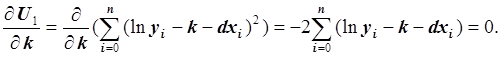
Умножив обе части уравнения на –0.5 и преобразовав, получим:

 .

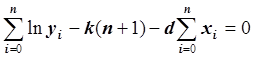Запишем это уравнение в виде:   .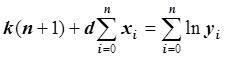

Второе уравнение:

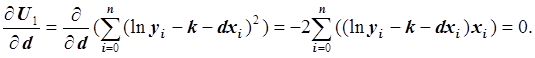
Умножив обе части уравнения на –0.5 и преобразовав, получим:

 .

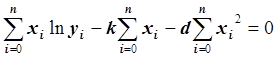Запишем это уравнение в виде:   .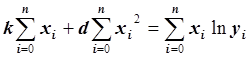

Получаем:

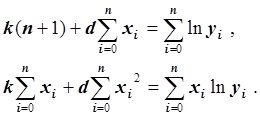
Мы получили систему линейных уравнений с симметричной невырожденной матрицей. Но это справедливо, если y_i > 0, 0 £ i £ n и c > 0 (функция ln x определена для     x > 0). Либо рассматриваются только такие данные (x_i, y_i), 0 £ i £ n, для которых y_i > 0, либо сначала от данных (x_i, y_i) нужно перейти к данным (x_i, z_i), 0 £ i £ n, где z_i = y_i+H,   H – положительная константа, выбранная таким образом, что z_i > 0, 0 £ i £ n.

Решая нормальную систему уравнений методом Гаусса с частичным выбором ведущего элемента, находим k и d. Затем находим c = exp(k). Отметим, что c > 0.

Замечание. При построении регрессионной функции можно полагать, что исходные данные (x_i, y_i), 0 £ i £ n, положительны. Если это не так, то всегда можно подобрать положительные числа T и H такие, что t_i = x_i + T > 0, z_i = y_i + H > 0, так как таблица данных (x_i, y_i) конечна. В результате получаем таблицу данных (t_i, z_i), 0 £ i £ n, с положительными значениями.

Для сведения нелинейной регрессии к линейной применяются линеаризующие преобразования и замена параметров. Линеаризующее преобразование F выбирается таким образом, чтобы функция g₁ = F(g(c₁, c₂,…, c_k, x)) была линейной функцией относительно некоторых параметров d₁, d₂,…, d_k.

Рассмотрим регрессионную функцию g(c, d, x) = 1/(c+dx). Линеаризующим преобразованием в данном случае является F(z) = 1/z. Получаем: g₁ = F(g) = c+dx. Функция g₁ = g₁(c, d, x) является линейной функцией относительно параметров c и d, поэтому не требуется вводить новые параметры. От функции U переходим к функции 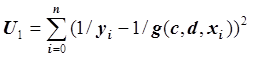. Отметим, что такой переход возможен, если y_i ¹ 0 и      g(c, d, x_i) ¹ 0, 0 £ i £ n.

Рассматривая функцию U₁ как функцию переменных c и d и используя необходимые условия экстремума функции нескольких переменных, получаем нормальную систему:

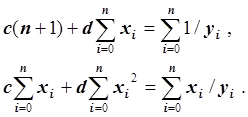
Мы получили систему линейных уравнений относительно неизвестных c и d с симметричной невырожденной матрицей. Решение этой системы линейных уравнений находится методом Гаусса с частичным выбором ведущего элемента.

Пример. Найти регрессионную функцию g(c, d, x) = cx/(d+x), описывающую связь между собой переменных x = (x₀, x₁,…, x_n) и y = (y₀, y₁,…, y_n).

Сначала применим линеаризующее преобразование F(z) = 1/z. Получаем              g₁ = F(g (c, d, x)) = (d+x)/cx = d/cx + 1/c. Полагая, что x_i ¹ 0, 0£ i £ n и c ¹ 0, введем новые параметры: k = 1/c и m = d/c. Функция g₁(k, m, x) = k+m/x является линейной функцией относительно параметров k и m. От функции U переходим к функции 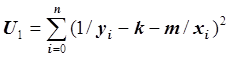, y_i ¹ 0, 0 £ i £ n.

Запишем нормальную систему:

 

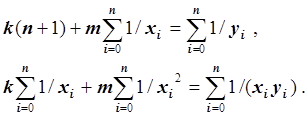
Мы получили систему линейных уравнений относительно неизвестных k и m с симметричной невырожденной матрицей. Решение этой системы уравнений находится методом Гаусса с частичным выбором ведущего элемента. Зная k и m, находим c = 1/k и d = m/k, k ¹ 0.

4.5. Примеры решения задач

Задача 1. Пусть заданы экспериментальные данные (x_i, y_i), 0 £ i £ n. Используя метод наименьших квадратов, построить алгоритм для нахождения регрессионной функции g(a, b, x) = a sin x + bx², описывающей связь между x и y.