Метод наименьших квадратов. Простая линейная регрессия, страница 14

Зная  ,  и , мы можем вычислить значение функции  для любого значения . Значения прогноза , ,  находятся по формуле , где  принимает значения 1, 2, 3.

На печать выводятся значения прогноза , , .

При решении задачи сглаживания среднеквадратичная погрешность вычисляется по формуле

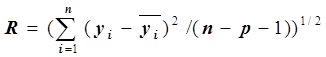, где – фактические значения уровней временного ряда;

– расчетные значения уровней временного ряда, ;

 – число уровней  во временном ряду;

– число параметров, входящих в формулу, описывающую тренд.

В нашем случае , n = 21.

Замечание. Обратить внимание, что в этом задании число заданных уровней временного ряда n различно у разных вариантов, и учесть это при программировании.

Программа

#include <stdio.h>

#include <math.h>

#include <conio.h>

int n=21; // число заданных уровней временного ряда

// Заданные уровни временного ряда Yi[n+1]

const float Yi[22]={ 0.0, 1.11, 1.24, 1.39, 1.55, 1.73, 1.92, 2.13, 2.36,

2.59, 2.84, 3.10, 3.37, 3.65, 3.95, 4.25, 4.56,

4.88, 5.21, 5.56, 5.91, 6.27

};  // элемент массива Yi[0]=0 в дальнейшем

                  // не используется, т.к. нумерация уровней

                  // временного ряда начинается с 1

// Функция f1(x)

float f1x (float A,float B,float C,float t)

{ return (A+B*t+C*t*t); }

// Функция GaussMethod - решает СЛУ размерности 3

// Входные параметры: А - матрица, В - вектор, Х - вектор неизвестных

void GaussMethod(float A[3][3],float B[3],float X[3])

{

int i,j; // счетчики циклов

// Решение системы уравнений

// k-счетчик циклов

// numb-номер строки с ведущим элементом

// max-максимальный по модулю элемент непреобразованного столбца

// str,bstr- используются при перестановке строк

// L-коэффициент преобразования

int numb=0, k;

float max, str, bstr, L;

// Приведение матрицы к U-виду

for (j=0;j<2;j++)

{

max=fabs(A[j][j]);

numb=j;

// Определение максимального элемента в столбце

for (i=j;i<3;i++)

{

if (max<fabs(A[i][j]))

{ max=fabs(A[i][j]); numb=i; };

};

// Если максимум - не диагональный элемент, то...

if (numb!=j)

{

// ...замена строк

for (i=0;i<3;i++)

{

str=A[numb][i];

A[numb][i]=A[j][i];

A[j][i]=str;

};

bstr=B[numb];

B[numb]=B[j];

B[j]=bstr;

};

// Преобразование столбца

for (i=j+1;i<3;i++)

{

L=-(A[i][j]/A[j][j]);//вычисление коэффициента

A[i][j]=0.0;

// Обнуление элемента текущего столбца

for (k=j+1;k<3;k++) { A[i][k]=A[i][k]+A[j][k]*L; };

// и вычисление последующих в строке

B[i]=B[i]+B[j]*L;

};

};

// Решение системы линейных уравнений

for (j=2;j>=0;j--)

{

X[j]=B[j]/A[j][j];

if (j!=2)

{

for (i=2;i>j;i--) {X[j]=X[j]-A[j][i]*X[i]/A[j][j];};

};

};

}

// Главная функция

void main()

{

clrscr();

int Ti[25];     // массив Ti[n+4], Ti[i] - номер уровня временного ряда

float Pi[25],   // массив Pi[n+4], Pi[i] - значение тренда

a[3][3], b[3], x[3];   // а - матрица, b - вектор,

// x - вектор незвестных

float A=0,B=0,C=0,  // искомые коэффициенты функции g(x)

R=0;            //среднеквадратичная погрешность

int p=3;  //число параметров, входящих в формулу, описывающую тренд

// Обнуление элементов матриц

for (int i=0;i<=n+3;i++)

{ Ti[i]=0; Pi[i]=0; }

// Заполнение массива Ti[i] значениями номеров уровней временного ряда

for(i=1;i<=n;i++) Ti[i]=i;

// Обнуление элементов матрицы а и вектора b

for(i=0;i<3;i++)

{

b[i]=0;

for(int j=0;j<3;j++) { a[i][j]=0;}

}

// Заполнение матрицы а и вектора b

for(i=1;i<=n;i++)

{

a[0][1]=a[0][1]+Ti[i];

a[0][2]=a[0][2]+Ti[i]*Ti[i];

a[1][2]=a[1][2]+Ti[i]*Ti[i]*Ti[i];

a[2][2]=a[2][2]+Ti[i]*Ti[i]*Ti[i]*Ti[i];

b[0]   =b[0]   +Yi[i];

b[1]   =b[1]   +Ti[i]*Yi[i];

b[2]   =b[2]   +Yi[i]*Ti[i]*Ti[i];

}

a[0][0]=n;

a[1][0]=a[0][1];

a[1][1]=a[0][2];

a[2][0]=a[0][2];

a[2][1]=a[1][2];

// Нахождение неизвестных х[3] методом Гаусса с ЧВВЭ

GaussMethod(a,b,x);

A=x[0];B=x[1];C=x[2];  //искомые коэффициенты A,B,C

// Сглаживание

for(i=1;i<=n;i++)

{

Pi[i]=f1x(A,B,C,Ti[i]);  //вычисление значений тренда для i от 1 до n

// Вычисление

R=R+pow(Yi[i]-Pi[i],2);

}

// Вычисление среднеквадратичной погрешности

R=sqrt(R/(n-p-1));

// Прогнозирование для i от n+1 до n+3

for(i=n+1;i<=n+3;i++)

{

Ti[i]=i;