Метод наименьших квадратов. Простая линейная регрессия, страница 13

for (j=2;j>=0;j--)

{

X[j] = B[j]/A[j][j];

if (j!=2)

{

for (i=2;i>j;i--) {X[j] = X[j]-A[j][i]*X[i]/A[j][j];};

};

};

}

// Главная функция

void main()

{

clrscr();

float Xi[21],Yi[21], // таблица данных

a[3][3],b[3],x[3];    // а - матрица, b - вектор,

                        // x - вектор неизвестных

float A=0,B=0,C=0;   // искомые параметры функции g(A, B, C, x)

float h=0;           // шаг

int n=20;            // число отрезков - n

float ai=-2,bi=3;    // отрезок [-2;3]

float R=0;           // значение среднеквадратичной погрешности

h = float(bi-ai)/n;  // вычисляем шаг

// Создание таблицы данных

for(int i=0;i<=n;i++)

{

Xi[i] = ai+i*h;

Yi[i] = fn(Xi[i]);

}

// Обнуление элементов матрицы а и вектора b

for(i=0;i<3;i++)

{

b[i] = 0;

for(int j=0;j<3;j++) { a[i][j] = 0;}

}

// Заполнение матрицы а и вектора b

for(i=0;i<=n;i++)

{

a[0][0] = a[0][0] + sin(Xi[i]) * sin(Xi[i]);

a[0][1] = a[0][1] + Xi[i] * sin(Xi[i]);

a[0][2] = a[0][2] + sin(Xi[i]);

a[1][1] = a[1][1] + Xi[i] * Xi[i];

a[1][2] = a[1][2] + Xi[i];

b[0]    = b[0]    + Yi[i] * sin(Xi[i]);

b[1]    = b[1]    + Xi[i] * Yi[i];

b[2]    = b[2]    + Yi[i];

}

a[2][2] = n+1;

a[1][0]=a[0][1];

a[2][0]=a[0][2];

a[2][1]=a[1][2];

// Нахождение неизвестных х[3] методом Гаусса с частичным выбором

//ведущего  элемента

GaussMethod(a,b,x);

A = x[0]; B = x[1]; C =x [2];  // искомые параметры A, B, C

                              // регрессионной функции g

// Расчет значений функции g  

float Gi[21];

for(i=0;i<=n;i++)

{

Gi[i] = gx(A,B,C,Xi[i]);

}

// Вычисление среднеквадратичной погрешности

for(i=0;i<=n;i++)

R=R+(Yi[i]-gx(A,B,C,Xi[i]))*(Yi[i]-gx(A,B,C,Xi[i]));

R=sqrt(R/(n+1));   

// Вывод значений

printf("Узлы сетки\tФункция f   Регрессионная функция g\n");

for(i=0;i<=n;i++)

printf("  %.2f   \t  %.2f \t\t   %.2f \n",Xi[i],Yi[i],Gi[i]);

printf("\n\nЗначение среднеквадратичной погрешности равно : %.2g",R);

getch();

}

Результаты работы программы

Узлы сетки  Функция f       Регрессионная функция g

-2.00        10.25              8.94

-1.75        9.55               8.88

-1.50        8.85               8.70

-1.25        8.17               8.39

-1.00        7.50               7.96

-0.75        6.84               7.43

-0.50        6.21               6.82

-0.25        5.59               6.14

0.00         5.00               5.43

0.25         4.44               4.73

0.50         3.91               4.05

0.75         3.43               3.44

1.00         3.00               2.91

1.25         2.63               2.48

1.50         2.33               2.17

1.75         2.11               1.99

2.00         2.00               1.93

2.25         2.01               1.98

2.50         2.16               2.12

2.75         2.48               2.35

3.00         3.00               2.62

Значение среднеквадратичной погрешности равно : 0.44

ПРИМЕР ВЫПОЛНЕНИЯ ЗАДАНИЯ 2

Задание. Построить алгоритм для нахождения прогноза с  по  уровень временного ряда ,  ,  методом наименьших квадратов для квадратичной модели. Разработать программу, которая реализует этот алгоритм и выводит на печать значения прогноза , , . Заданы , ,  и : 1.11; 1.24; 1.39; 1.55; 1.73; 1.92; 2.13; 2.36; 2.59; 2.84; 3.10; 3.37; 3.65; 3.95; 4.25; 4.56; 4.88; 5.21; 5.56; 5.91; 6.27; n = 21.

Решение. В данном случае требуется решить задачу прогноза. Решим эту задачу следующим образом. Сначала, используя метод наименьших квадратов, найдем решение задачи сглаживания – тренд . А затем, используя формулу тренда, найдем решение задачи прогноза: ,  . В дальнейшем будем опираться на материал, изложенный в п.п. 5.3.

Задано, что тренд является параболической функцией, следовательно, . Коэффициенты ,  и  находятся методом наименьших квадратов. В примере выполнения задания 1 расчетно-графического задания 2 подробно разбирался алгоритм построения нормальной системы, поэтому сразу запишем систему линейных уравнений для нахождения неизвестных ,  и :

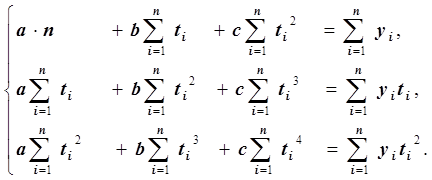
Эта система линейных уравнений имеет единственное решение, которое находится методом Гаусса с частичным выбором ведущего элемента.