Коэффициент корреляции
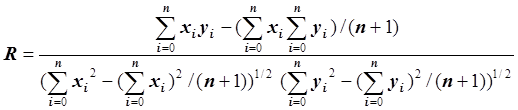
характеризует степень отклонения связи между x = (x0, x1,…, xn) и y = (y0, y1,…, yn) от линейной. Если |R| близок к единице, то эта связь близка к линейной (т.е. выбор линейной функции в качестве регрессионной модели оказался удачным). Причем знак коэффициента корреляции R определяет знак параметра c2. Если R>0, то c2>0, если R<0, то c2<0 /2/. Если R близок к 0 (R » 0), то говорят, что отсутствует линейная связь между x = (x0, x1,…, xn) и y = (y0, y1,…, yn). В этом случае возможна нелинейная зависимость между x и y. Если |R|<0.3, то линейная связь считается слабой, если |R|>0.7, то линейная связь считается сильной /5/.
4.3. Простая нелинейная регрессия
Следует выделить два класса нелинейных регрессионных функций.
1. Регрессионные функции g(c1, c2,…, ck, x), являющиеся линейными функциями относительно параметров c1, c2,…, ck, но нелинейными функциями относительно переменной x. Например,
g(c1, c2, x) = c1+c2x2 ,
g(c1, c2, c3, x) = c1+c2×sin x+c3x4 .
2. Регрессионные функции, являющиеся нелинейными функциями относительно параметров c1, c2,…, ck. Например,
![]() ,
,
g(c1, c2, x) = 1/(c1+c2x) .
Принципиальное отличие этих двух классов заключается в том, что в первом случае методом наименьших квадратов мы получаем систему линейных уравнений с симметричной матрицей, которая является невырожденной при некоторых ограничениях на функцию g, а во втором случае методом наименьших квадратов мы получаем систему нелинейных уравнений. Для получения системы линейных уравнений во втором случае следует предварительно применить линеаризирующие преобразования, а затем уже использовать метод наименьших квадратов.
В данном подпункте мы будем рассматривать только первый класс нелинейных регрессионных функций, а второй класс рассмотрим в следующем подпункте.
Рассмотрим случай k = 3, т.е. регрессионная функция g(c1, c2,…, ck, x) является функцией ![]() , где m(x),
s(x) и r(x) – некоторые гладкие линейно
независимые функции. В дальнейшем мы будем использовать следующие обозначения: a = c1, b =
c2,
c = c3, таким образом,
получаем:
, где m(x),
s(x) и r(x) – некоторые гладкие линейно
независимые функции. В дальнейшем мы будем использовать следующие обозначения: a = c1, b =
c2,
c = c3, таким образом,
получаем:
![]() .
.
Применим метод наименьших квадратов для нахождения
параметров a, b и c,
т.е. будем искать такие числа a, b и c,
при которых функция 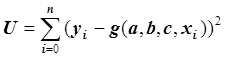 достигает минимума, т.е.:
достигает минимума, т.е.:
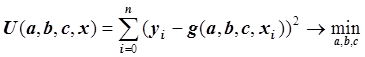 .
.
Рассматривая функцию U как функцию переменных a, b и c и используя необходимые условия экстремума функции нескольких переменных, получаем нормальную систему уравнений:
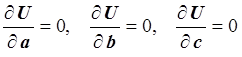 .
.
Так как функция g является линейной функцией относительно a, b и c, то получаем систему линейных уравнений. Запишем первое уравнение:
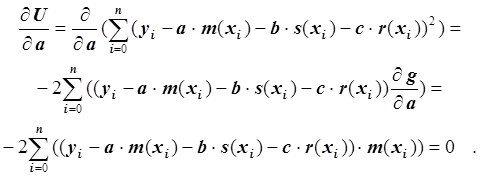
Умножив обе части уравнения на –0.5 и преобразовав, получим:
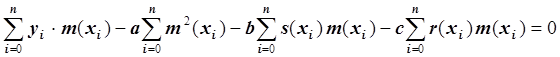 .
.
Запишем это уравнение в виде:
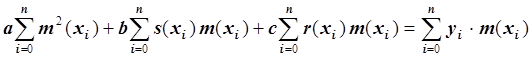 .
.
Второе уравнение:
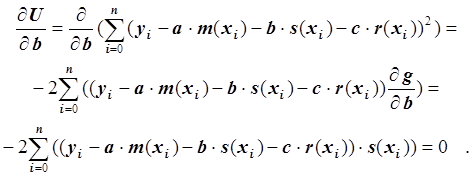
Умножив обе части уравнения на –0.5 и преобразовав, получим:
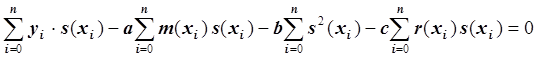 .
.
Запишем это уравнение в виде:
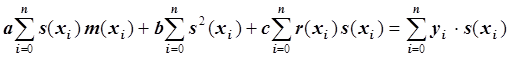 .
.
Третье уравнение:
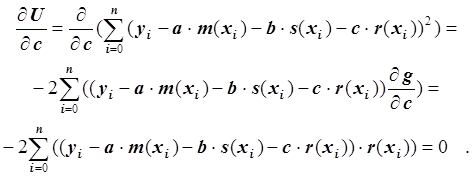
Умножив обе части уравнения на –0.5 и преобразовав, получим:
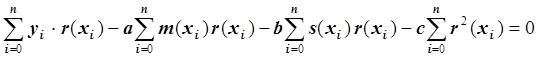 .
.
Запишем это уравнение в виде:
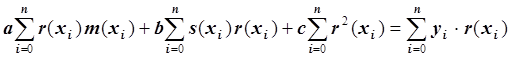 .
.
Запишем систему линейных уравнений:
![]()
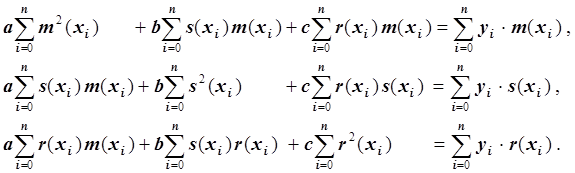
Мы получили систему линейных уравнений с симметричной матрицей. Если функции {m(x), s(x), r(x)} линейно независимы, то эта матрица будет невырожденной. Для нахождения a, b и c решаем систему линейных уравнений методом Гаусса с частичным выбором ведущего элемента.
4.4. Регрессия, нелинейная относительно параметров
Если регрессионная функция g(c1, c2,…, ck, x) является нелинейной функцией относительно c1, c2,…, ck, x, то сначала нужно применить линеаризующие преобразования, а затем уже использовать метод наименьших квадратов.
Пример. Рассмотрим задачу нахождения регрессионной функции g = g(c, d, x) = = c exp(dx), описывающей связь между собой двух переменных x = (x0, x1,…, xn) и y = (y0, y1,…, yn).
Сначала применим линеаризующее преобразование F(z)
= ln(z).
Получим: g1
= = ln g = ln с + dx. Вводим
новый параметр k = ln c и получаем функцию g1, линейную
относительно параметров k и d: g1 = ln g
= k + dx. Вместо функции 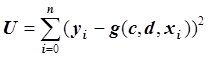 получаем
функцию
получаем
функцию 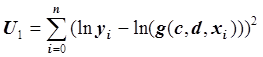 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.