Метод наименьших квадратов. Простая линейная регрессия, страница 7

На практике по имеющемуся временному ряду задают вид тренда (трендовой функции)  f(t) и находят параметры f(t), а затем анализируют поведение отклонений от тенденции /5/. Трендовые функции, построенные методом наименьших квадратов, сравниваются между собой по величине среднеквадратичной ошибки, вычисляемой по формуле

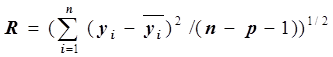, где         y_i– фактические значения уровней временного ряда;

– расчетные значения уровней временного ряда, ;

n – число уровней  во временном ряду;

p – число параметров, входящих в формулу, описывающую тренд.

Отметим, что для линейной зависимости p = 2, а для параболической (квадратичной) зависимости p = 3.

Программа для решения задач сглаживания и прогноза приведена в примере выполнения задания 2 расчетно–графического задания 2.

РАСЧЕТНО-ГРАФИЧЕСКОЕ ЗАДАНИЕ 1

Задание 1. Построить алгоритм для интерполяции функции  на отрезке  интерполяционным линейным сплайном  с равномерным шагом. Разработать программу, которая реализует этот алгоритм и выводит на печать значение сплайна  и значение функции , значение производной сплайна и производной функции при . Размерность интерполяционной таблицы равна 21.

Задание 2. Построить алгоритм для интерполяции функции  на отрезке  естественным интерполяционным кубическим сплайном  с равномерным шагом. Разработать программу, которая реализует этот алгоритм и выдает на печать значение сплайна  и функции , значение производной сплайна и производной функции при . Размерность интерполяционной таблицы равна 21.

Варианты заданий

ПРИМЕР ВЫПОЛНЕНИЯ ЗАДАНИЯ 1