1. Метод прогонки
Метод
прогонки – это метод решения систем линейных уравнений с ленточными матрицами,
т.е. матрицами, большая часть элементов которых равна нулю, а ненулевые
элементы расположены на нескольких диагоналях. Более строго, матрица, для элементов
которой выполняется условие ![]() , если
, если ![]() , называется ленточной. В дальнейшем мы будем рассматривать
только трехдиагональные и пятидиагональные ленточные матрицы.
, называется ленточной. В дальнейшем мы будем рассматривать
только трехдиагональные и пятидиагональные ленточные матрицы.
Использование
метода Гаусса для решения систем линейных уравнений с ленточными матрицами
нерационально, так как большая часть времени работы программы будет тратиться
на обработку нулевых элементов. Метод прогонки можно рассматривать как частный
случай метода Гаусса, в котором учитывается то, что большая часть элементов
матрицы равна нулю. Напомним, что для реализации метода Гаусса требуется ![]() арифметических
действий, где
арифметических
действий, где ![]() - число линейных уравнений, а для реализации метода
прогонки требуется
- число линейных уравнений, а для реализации метода
прогонки требуется ![]() арифметических действий.
арифметических действий.
1.1. МЕТОД ПРОГОНКИ ДЛЯ ТРЕХДИАГОНАЛЬНЫХ МАТРИЦ
Запишем
систему линейных уравнений ![]() с трехдиагональной матрицей:
с трехдиагональной матрицей:
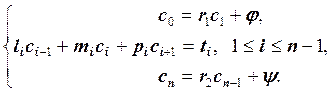
Или в виде:
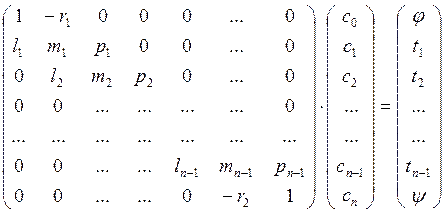
Рассмотрим метод прогонки для матрицы с диагональным
преобразованием, то есть для таких квадратных матриц ![]() , для
которых выполняются неравенства:
, для
которых выполняются неравенства:
![]() ,
, ![]() ,
, ![]() .
.
Напомним, что матрица с диагональным преобладанием невырожденна.
Для трехдиагональной матрицы, рассмотренной выше, условия диагонального преобладания записываются следующим образом:
![]()
Для матрицы с диагональным преобладанием метод прогонки – это частный случай метода Гаусса, в котором автоматически используется в качестве ведущего элемента максимальный по модулю элемент в строке и учитывается тот факт, что большая часть элементов матрицы равна нулю.
Идея метода прогонки заключается в том, что
неизвестное ![]() представляется в виде:
представляется в виде: ![]() ,
, ![]() , где
, где ![]() и
и ![]() - неизвестные числовые коэффициенты, называемые прогоночными
коэффициентами.
Почему именно в таком виде? Напомним, что метод прогонки – это частный случай
метода Гаусса, а в методе Гаусса после выполнения прямого хода метода Гаусса мы
получаем систему линейных уравнений с верхней треугольной матрицей. В случае
трехдиагональной матрицы, после выполнения прямого хода метода Гаусса мы
получаем двухдиагональную матрицу с ненулевыми ведущими элементами:
- неизвестные числовые коэффициенты, называемые прогоночными
коэффициентами.
Почему именно в таком виде? Напомним, что метод прогонки – это частный случай
метода Гаусса, а в методе Гаусса после выполнения прямого хода метода Гаусса мы
получаем систему линейных уравнений с верхней треугольной матрицей. В случае
трехдиагональной матрицы, после выполнения прямого хода метода Гаусса мы
получаем двухдиагональную матрицу с ненулевыми ведущими элементами:
![]() ,
, ![]() . Разделив на
. Разделив на ![]() и оставив в левой части только
и оставив в левой части только ![]() , получаем
, получаем ![]() .
.
Приведем формулы метода прогонки.
1.
На первом
этапе находим ![]() .
.
2. Затем, в порядке возрастания индексов, находим остальные прогоночные коэффициенты по формулам:
![]() ,
, ![]() , где
, где ![]() .
.
Первые два этапа называют прямой прогонкой. Отметим, что они аналогичны прямому ходу метода Гаусса.
3. Находим неизвестное ![]() :
: ![]()
4. Находим неизвестные ![]() в порядке убывания индексов:
в порядке убывания индексов:
![]() ,
, ![]()
Два последних этапа называют обратной прогонкой.
Рассмотрим устойчивость метода прогонки.
Формулы метода прогонки можно применять, если знаменатели дробей при вычислении
![]() ,
, ![]() ,
, ![]() не обращаются в ноль. Кроме того, если
не обращаются в ноль. Кроме того, если ![]() , то при вычислениях
, то при вычислениях ![]() возможно накопление погрешностей.
возможно накопление погрешностей.
Теорема (корректность и устойчивость метода
прогонки). Если
выполняются неравенства ![]() то знаменатели дробей в методе прогонки не
обращаются в ноль, и метод прогонки является устойчивым
то знаменатели дробей в методе прогонки не
обращаются в ноль, и метод прогонки является устойчивым ![]() .
.
Число арифметических действий, необходимых
для реализации метода прогонки, пропорционально числу неизвестных - ![]() . Таким образом, у метода прогонки два достоинства:
малое число арифметических действий для его реализации и слабая
чувствительность к вычислительным погрешностям.
. Таким образом, у метода прогонки два достоинства:
малое число арифметических действий для его реализации и слабая
чувствительность к вычислительным погрешностям.
1.2. МЕТОД ПРОГОНКИ ДЛЯ ПЯТИДИАГОНАЛЬНЫХ МАТРИЦ
Рассмотрим метод прогонки для пятидиагональных матриц с диагональным преобладанием. Запишем систему линейных уравнений:
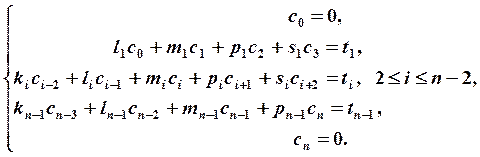
Именно в таком виде записывается система линейных уравнений при нахождении коэффициентов естественного сглаживающего кубического сплайна.
Будем полагать, что выполняются условия диагонального преобладания:
![]()
![]()
Напомним, что при выполнении этих условий система линейных уравнений имеет единственное решение.
Идея метода прогонки для пятидиагональных
матриц заключается в том, что неизвестное ![]() представляется в виде:
представляется в виде: ![]() ,
, ![]() , где
, где ![]() ,
, ![]() и
и ![]() - неизвестные числовые коэффициенты, называемые прогоночными
коэффициентами.
- неизвестные числовые коэффициенты, называемые прогоночными
коэффициентами.
Приведем формулы метода прогонки.
1. На первом этапе находим значения
![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
2. Затем, в порядке возрастания индексов, находим остальные прогоночные коэффициенты по формулам:
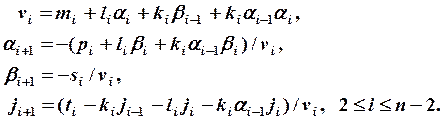
Первые два этапа называют прямой прогонкой.
3.
Находим
неизвестные ![]() и
и ![]() :
: ![]()
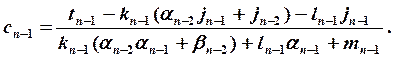
4.
Находим
неизвестные ![]() в порядке убывания индексов:
в порядке убывания индексов:
![]() ,
, ![]()
Два последних этапа называют обратной прогонкой.
2. СПЛАЙН – ИНТЕРПОЛЯЦИЯ
Напомним основные определения.
Определение сетки.Рассмотрим отрезок ![]() и конечное множество, состоящее из точек
и конечное множество, состоящее из точек ![]() , удовлетворяющих следующему условию:
, удовлетворяющих следующему условию:
![]() .
.
Множество
точек ![]() называется сеткой на отрезке
называется сеткой на отрезке ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.