Сложность вычислительного алгоритма построения интерполяционного кубического сплайна та
же, что и у параболического и линейного сплайнов. Число арифметических
действий, необходимых для построения интерполяционного кубического сплайна,
пропорционально числу отрезков (![]() ), объем памяти также
пропорционален числу отрезков (
), объем памяти также
пропорционален числу отрезков (![]() ).
).
Так как интерполяционный кубический сплайн хорошо приближает гладкие функции (теорема о сходимости, оценка погрешности) и имеет минимальную сложность, то на практике для гладких функций при решении задач интерполяции и численного дифференцирования используется именно интерполяционный кубический сплайн.
2.4. B-СПЛАЙНЫ
B-сплайны (базовые, фундаментальные, базисные сплайны)
– это функции,
определенные на отрезке ![]() и образующие некоторый
базис, который позволяет представить любой сплайн в виде линейной комбинации
соответствующих B-сплайнов. Так же, как произвольный вектор
и образующие некоторый
базис, который позволяет представить любой сплайн в виде линейной комбинации
соответствующих B-сплайнов. Так же, как произвольный вектор ![]() , принадлежащий плоскости
, принадлежащий плоскости ![]() , можно единственным образом представить в
виде линейной комбинации базисных векторов
, можно единственным образом представить в
виде линейной комбинации базисных векторов ![]() и
и ![]() , а именно
, а именно ![]() , так и
произвольный сплайн можно единственным образом представить в виде линейной
комбинации соответствующих базисных сплайнов.
, так и
произвольный сплайн можно единственным образом представить в виде линейной
комбинации соответствующих базисных сплайнов.
B-сплайном нулевой степени, построенным на отрезке ![]() по сетке
по сетке ![]() ,
называется функция вида:
,
называется функция вида:
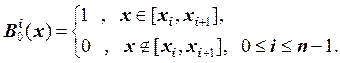
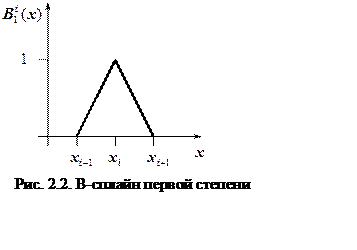 B-сплайн
B-сплайн
![]() степени
степени ![]() может
быть отличен от нуля только на
может
быть отличен от нуля только на ![]() отрезках
отрезках ![]() , примыкающих друг к другу. Например,
кубический B-сплайн
, примыкающих друг к другу. Например,
кубический B-сплайн ![]() отличен от нуля на отрезке
отличен от нуля на отрезке ![]() , а линейный B – сплайн отличен от нуля на
отрезке
, а линейный B – сплайн отличен от нуля на
отрезке ![]() (рис. 2.2).
(рис. 2.2).
Любой линейный сплайн на отрезке ![]() можно представить в виде линейной
комбинации B-сплайнов первой степени:
можно представить в виде линейной
комбинации B-сплайнов первой степени:
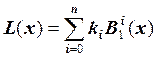 .
.
Любой кубический сплайн на отрезке ![]() также может быть единственным образом
представлен в виде линейной комбинации кубических B-сплайнов. Такой подход
позволяет уменьшить объем памяти, необходимый для построения сплайна.
также может быть единственным образом
представлен в виде линейной комбинации кубических B-сплайнов. Такой подход
позволяет уменьшить объем памяти, необходимый для построения сплайна.
2.5. ПОСТРОЕНИЕ ИНТЕРПОЛЯЦИОННЫХ СПЛАЙНОВЫХ КРИВЫХ ПРИ ПОМОЩИ СПЛАЙН - ФУНКЦИЙ
 Ранее
мы всегда оговаривали, что в интерполяционной таблице все узлы сетки
Ранее
мы всегда оговаривали, что в интерполяционной таблице все узлы сетки ![]() различны и упорядочены по возрастанию
различны и упорядочены по возрастанию ![]() . Как строить интерполяционные сплайны,
если узлы сетки совпадают между собой или не упорядочены по возрастанию? В
таких случаях решением задачи интерполяции являются кривые, заданные
параметрически
. Как строить интерполяционные сплайны,
если узлы сетки совпадают между собой или не упорядочены по возрастанию? В
таких случаях решением задачи интерполяции являются кривые, заданные
параметрически ![]() Приведем алгоритм для
описания параметрических уравнений кривой, описанный в книге / 9 /.
Приведем алгоритм для
описания параметрических уравнений кривой, описанный в книге / 9 /.
Пусть задана интерполяционная
таблица ![]() ,
, ![]() , причем узлы сетки
, причем узлы сетки ![]() не упорядочены и могут совпадать между
собой. Требуется построить кривую, последовательно проходящую через все точки
интерполяционной таблицы.
не упорядочены и могут совпадать между
собой. Требуется построить кривую, последовательно проходящую через все точки
интерполяционной таблицы.
1. На
произвольном отрезке ![]() изменения
параметра
изменения
параметра ![]() вводится
вспомогательная сетка, узлы которой упорядочены и различны:
вводится
вспомогательная сетка, узлы которой упорядочены и различны: ![]() . Число узлов сетки совпадает с числом
заданных точек
. Число узлов сетки совпадает с числом
заданных точек ![]() . В качестве отрезка
. В качестве отрезка ![]() можно выбрать отрезок [0,1], а шаг
можно выбрать отрезок [0,1], а шаг ![]() по переменной
по переменной ![]() выбрать равномерный, т.е.
выбрать равномерный, т.е. ![]() .
.
2. По
известной интерполяционной таблице ![]() ,
, ![]() и вспомогательной сетке строятся две
вспомогательные интерполяционные таблицы:
и вспомогательной сетке строятся две
вспомогательные интерполяционные таблицы:
![]() ,
, ![]() ,
, ![]() .
.
Отметим, что в
построенных вспомогательных интерполяционных таблицах узлы сетки упорядочены и
различны, и по этим таблицам единственным образом могут быть построены
интерполяционные сплайны ![]() и
и ![]() .
.
3. По каждой
из вспомогательных интерполяционных таблиц строятся соответствующие
интерполяционные сплайн – функции ![]() и
и ![]() .
.
Таким образом, получается кривая, последовательно проходящая через все точки заданной интерполяционной таблицы (рис. 2.3).
2.6. ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача 1. По данной интерполяционной таблице построить интерполяционный линейный сплайн.
Решение. Пусть задана интерполяционная таблица:
|
|
0 |
1 |
2 |
|
|
3 |
2 |
5 |
Таким образом, задано ![]() ,
, ![]() ,
, ![]() и
и ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Линейный сплайн в данном случае (![]() ) определяется формулой:
) определяется формулой:
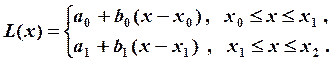
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.