Метод прогонки для трехдиагональных матриц, страница 8

Для нахождения коэффициентов  и  воспользуемся формулами  и ,   . Получаем ,  ,   ,   . Запишем

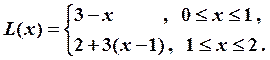
Проверим, что  - интерполяционный сплайн, для этого вычислим значения  при  Получаем ,   ,   , следовательно,  - интерполяционный сплайн.

Ответ: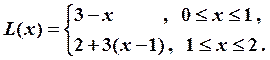   

Задача 2. Построить систему линейных уравнений для нахождения коэффициентов интерполяционного параболического сплайна по заданной интерполяционной таблице и краевому условию.

         Решение. Пусть задана интерполяционная таблица

	0	1	2
	3	2	7

и краевое условие: , т.е. , ,  ; , , , .

Решением задачи заключается в построении системы линейных уравнений относительно коэффициентов параболического сплайна . Так как , то параболический сплайн записывается следующим образом:

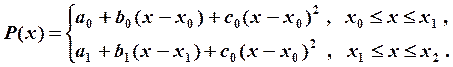
Неизвестных коэффициентов ,  и шесть, требуется записать шесть линейных уравнений. Первые три уравнения вытекают из условий: ,  . Получаем: ,  ,  , где ,   . В нашем случае равномерный шаг  равен 1. Получаем три уравнения: ,   ,   .

Одно уравнение вытекает из краевого условия . Запишем формулу для производной сплайна:

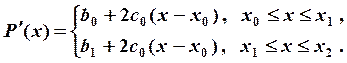
Из краевого условия получаем уравнение  или . Еще два уравнения получаем из условия, что параболический сплайн является непрерывно дифференцируемой функцией во всех внутренних узлах сетки. В нашем случае один  внутренний узел, а именно узел . Запишем формулу сплайна в виде:

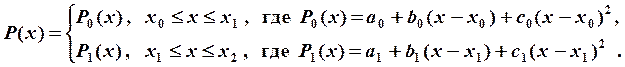
Из непрерывности сплайна вытекает уравнение  или , а из непрерывности производной сплайна вытекает, что  или .

Ответ:    Запишем систему линейных уравнений:

           

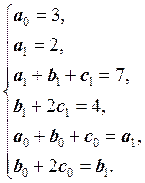
Отметим, что мы рассмотрели случай правого краевого условия (). Случай левого краевого условия рассматривается аналогично. Например, если вместо условия  задано условие , то в системе линейных уравнений четвертое уравнение нужно заменить на следующее: .

         Задача 3. Построить систему линейных уравнений для нахождения коэффициентов интерполяционного кубического сплайна по заданным краевым условиям и интерполяционной таблице.

Решение. Пусть задана интерполяционная таблица

	0	1	2
	2	5	6

и краевые условия:  и , т.е. , , , , , , , . Требуется построить систему линейных уравнений относительно коэффициентов кубического сплайна . Так как , то кубический сплайн записывается следующим образом:

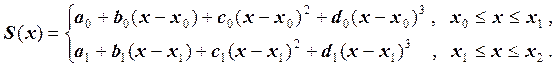
Неизвестных коэффициентов восемь, требуется записать восемь линейных уравнений. Первые три уравнения вытекают из условий ,  . Получаем: ,  ,  . Запишем первые три уравнения: ,   ,   .

Два уравнения вытекают из краевых условий. Запишем формулу для производной сплайна:

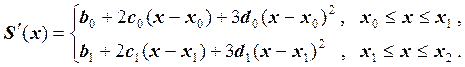
Из левого краевого условия  вытекает уравнение . Из правого условия  вытекает уравнение . Еще три уравнения получаем из условия, что кубический сплайн является дважды непрерывно дифференцируемой функцией во всех точках отрезка , в том числе и во внутренних узлах сетки. В нашем случае один внутренний узел, а именно узел . Запишем формулу сплайна в виде:

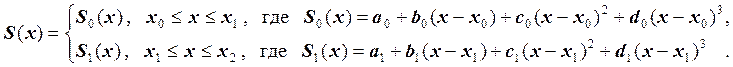
Из непрерывности сплайна вытекает уравнение . А из непрерывности первой и второй производной сплайна следуют уравнения  и . Получаем:

,   ,   .

Ответ:    Запишем систему линейных уравнений:

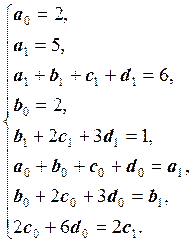
Задача 4. Определить, является ли функция  линейным сплайном, где

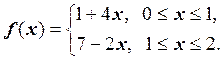
         Решение. Запишем функцию  в виде:

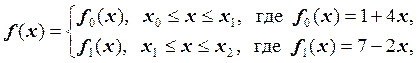
. Для того чтобы функция  являлась линейным сплайном, одновременно должны выполняться два условия:

1)  функции  и  - полиномы первой степени;

2)  функция  - непрерывная функция на отрезке