Метод прогонки для трехдиагональных матриц, страница 2

Сетка – это одно из основных понятий. Точки , , называются узлами сетки. Отметим, что в дальнейшем мы будем рассматривать только такие сетки, в которых все узлы сетки различны ( для ) и упорядочены по возрастанию.

Определение интерполяционной таблицы.Пусть заданы вещественные числа . Таблица, состоящая из значений , , называется интерполяционной таблицей, где  - узлы сетки,  – значения некоторой функции в узлах сетки.

Постановка задачи интерполяции. Пусть на отрезке  задана сетка , в узлах которой заданы значения: , , (где  - некоторая функция). Требуется построить функцию  такую, что

1) ,               ;

2)  достаточно близка к  на отрезке .

Другими словами, задача интерполяции заключается в нахождении значений таблично заданной функции в тех точках внутри заданного отрезка, которые не являются узлами сетки.

Постановка задачи численного дифференцирования. Пусть на отрезке  задана сетка , в узлах которой заданы значения: ,  (где  - некоторая функция). Требуется найти функцию  на отрезке , которая достаточно близка к .

В курсе «Вычислительная математика» мы рассматривали интерполяцию полиномами, в дальнейшем мы будем изучать сплайн-интерполяцию. При решении задачи интерполяции будем полагать, что  - интерполяционный сплайн. При решении задачи численного дифференцирования будем полагать, что  - производная некоторого сплайна. При этих предположениях о функциях  и  задачи интерполяции и численного дифференцирования имеют единственное решение.

Сначала мы дадим нестрогое определение сплайна, а затем подробно рассмотрим интерполяционный линейный сплайн, интерполяционный параболический сплайн и интерполяционный кубический сплайн.

Сплайнна отрезке  - это функция (как правило, непрерывная), которая является кусочно-полиномиальной, то есть состоит из «кусочков» полиномов одинаковой степени.

Рекомендуемая литература: / 7 – 9 /.

2.1. ИНТЕРПОЛЯЦИОННЫЙ ЛИНЕЙНЫЙ СПЛАЙН

Линейный сплайнна отрезке  - это непрерывная кусочно-линейная функция. На отрезке  введем сетку . Обозначим  линейный сплайн. Для каждого  из отрезка  линейный сплайн определяется следующим образом: , где  и  - числовые коэффициенты.

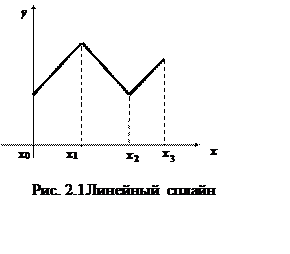Пример .           На рисунке 2.1 приведен график линейного сплайна. Формула этого сплайна записывается следующим образом:

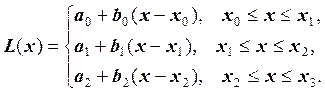
В дальнейшем мы будем рассматривать, как правило, равномерные сетки . Так как сетка  состоит из  точки, то отрезок  разбит на  отрезков . На каждом из отрезков  линейный сплайн  определяется формулой , то есть однозначно определяется двумя коэффициентами: , . На всем отрезке  линейный сплайн  определяется  коэффициентами  и , . Для того, чтобы однозначно определить интерполяционный линейный сплайн на отрезке , нам требуется  уравнений относительно  и .

Так как  является интерполяционной функцией, то первые  уравнения получаем из условия , .

Узлы сетки  и  называют граничными узлами, а узлы  - внутренними узлами сетки. Во всех внутренних узлах сетки (а их число равно ) функция  должна быть непрерывна, следовательно, получаем еще  уравнение. В сумме получаем  линейных уравнений относительно  неизвестных  и .

Дадим строгое определение интерполяционного линейного сплайна.

Определение интерполяционного линейного сплайна.    Пусть на отрезке  задана сетка , в узлах которой заданы значения ,. Интерполяционным линейным сплайном называется функция , удовлетворяющая следующим условиям:

1)  функция  – непрерывная функция на  ;

2)  на каждом из отрезков  функция  является полиномом первой степени вида

, ;

3)  функция  – интерполяционная функция, то есть: , .

Отметим, что из этого определения, отбросив условие три, мы получаем определение линейного сплайна.

Пример.  Функция

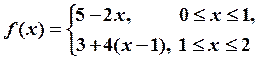
является линейным сплайном, определенным на отрезке . Эта же функция является интерполяционным линейным сплайном, удовлетворяющим следующей интерполяционной таблице: