Метод прогонки для трехдиагональных матриц, страница 6

Пример.  Функция

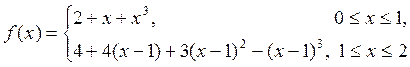
является естественным кубическим сплайном, определенным на отрезке . Эта же функция является естественным интерполяционным кубическим сплайном, удовлетворяющим следующей интерполяционной таблице:

	0	1	2
	2	4	10

Пример программы, которая по интерполяционной таблице строит естественный интерполяционный кубический сплайн, приводится в примере выполнения задания 2 расчетно-графического задания 1.

Теорема существования и единственности.        Пусть на отрезке  задана интерполяционная таблица , , причем все узлы сетки различны ( при ). Тогда существует единственный естественный кубический сплайн  такой, что .

Другими словами, если задана интерполяционная таблица, в которой все узлы сетки различны, то существует единственный естественный интерполяционный кубический сплайн, удовлетворяющий этой таблице.

Нахождение коэффициентов естественного интерполяционного

кубического сплайна

Из определения естественного интерполяционного кубического сплайна мы получаем систему линейных уравнений с невырожденной матрицей, число уравнений равно . Если мы будем решать эту систему линейных уравнений методом Гаусса с частичным выбором ведущего элемента, то нам потребуется  арифметических действий и  памяти. Но известен устойчивый алгоритм нахождения коэффициентов сплайна, для реализации которого требуется  арифметических действий и  памяти. Опишем этот алгоритм.

1.  По явным формулам находятся коэффициенты , .

2.  Коэффициенты  находятся из решения системы линейных уравнений размерности  с невырожденной трехдиагональной матрицей методом прогонки. Запишем эту систему линейных уравнений для случая равномерного шага

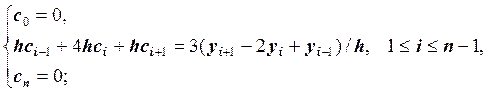
Условие  на применение метода прогонки для решения этой системы уравнений  следующее: . Это условие выполнено, если все узлы сетки различны.

3.  Зная  и , находим коэффициенты  и  по явным формулам:

,    ,   .

Отметим, что для удобства записи системы линейных уравнений, определен дополнительный коэффициент , равный нулю. Уравнения   и  вытекают из равенства нулю второй производной естественного интерполяционного кубического сплайна на концах отрезка .

Теорема (о сходимости). Пусть функция  - непрерывная функция на отрезке , тогда интерполяционный кубический сплайн  сходится к  при , стремящемся к нулю, для любой точки  из отрезка , то есть , где ,  .

Теорема (оценка погрешности). Пусть . Тогда для любой точки  справедливы следующие оценки погрешности:

,   ,   , где , а положительные константы , , и  не зависят от .

Таким образом, при уменьшении равномерного шага  в два раза, погрешность интерполяции кубическим сплайном уменьшается в 16 раз.

Производная интерполяционного кубического сплайна – это непрерывно дифференцируемая кусочно-параболическая функция, то есть параболический сплайн:

,   ,   .

Отметим, что производная интерполяционного кубического сплайна не является интерполяционным сплайном для производной функции.

Нахождение значений естественного интерполяционного

кубического сплайна и его производных

Как и для параболического сплайна, сначала находим номер  отрезка, содержащего точку , по формуле . Зная все коэффициенты , , ,  и номер отрезка , находим значение естественного интерполяционного кубического сплайна в точке, принадлежащей отрезку ,

.

Для вычисления значений сплайна и его производных в точке , введем дополнительные коэффициенты:  ,   ,   . Ранее уже был определен коэффициент .

Значения первой и второй производных естественного интерполяционного кубического сплайна вычисляются по формулам:

,   .