Метод прогонки для трехдиагональных матриц, страница 10

Узлы сетки  находятся по формуле ,  . Значения  находятся по формуле ,  . Таким образом, по формуле функции  на отрезке  построена интерполяционная таблица  размерности 21 с равномерным шагом. Так как все узлы сетки различны, то существует единственный интерполяционный кубический сплайн , удовлетворяющий этой таблице.

Для построения сплайна  сначала найдем его коэффициенты. Коэффициенты  находятся по явным формулам ,  . Для нахождения коэффициентов ,  , решается система линейных уравнений с трехдиагональной матрицей:

  ,

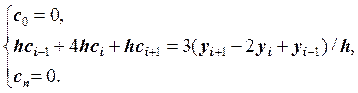
Эта система линейных уравнений имеет единственное решение, которое находится методом прогонки. Запишем формулы метода прогонки для данного примера. Сначала в порядке возрастания находятся прогоночные коэффициенты  и :

,   ,   ,   ,   , где   .

Затем в порядке убывания находятся неизвестные :

,   ,  

После нахождения коэффициентов  и , находим по явным формулам коэффициенты  и :

,    ,    ,

,   

Зная коэффициенты сплайна , мы можем найти его значение и значение его производной  в любой точке  из отрезка . Находим номер  отрезка, которому принадлежит точка, по формуле . Значение сплайна  при  находим по формуле

Значение производной сплайна при  находим по формуле

.

Программа

#include <stdio.h>

#include <conio.h>

#include <math.h>

float A,B;                         // границы отрезка

float Xi[21],Yi[21];               // интерполяционная таблица

float Ai[21],Bi[21],Ci[21],Di[21]; // коэффициенты ai, bi, ci, di

float Alpha[21],Betta[21];         // прогоночные коэффициенты

float h;                           // шаг сетки

float n;                           // число отрезков

// Функция sin(x)

float fn (float x) { return (sin(x)); }

// Производная функции sin(x)

float fsh (float x) { return (cos(x)); }

// Вычисление значений сплайна S(x)

float Sx (float x)

{

int i=int((x-A)/h);

return Ai[i]+Bi[i]*(x-Xi[i])+Ci[i]*(x-Xi[i])*(x-Xi[i])+Di[i]*(x-Xi[i])*

(x-Xi[i])*(x-Xi[i]);

}

// Вычисление значений производной сплайна

float Sshx (float x)

{

int i=int((x-A)/h);

return Bi[i]+2*Ci[i]*(x-Xi[i])+3*Di[i]*(x-Xi[i])*(x-Xi[i]);

}

void main()

{

clrscr();

float Ti=0;            // вспомогательная  переменная ti

// Инициализация начальных значений

A=-2,B=2;              // отрезок [-2,2]

n=20;                  // число отрезков n

h=float(B-A)/n;        // шаг

// Создание интерполяционной таблицы

for(int i=0;i<=n;i++)

{

Xi[i] = A+i*h;

Yi[i] = fn(Xi[i]);

}

// Находим коэффициенты сплайна ai, bi, ci, di

// Расчет коэффициентов ai

for(i=0;i<=n;i++) Ai[i]=Yi[i];

// Решение СЛУ с трехдиагональной матрицей методом прогонки

//                          для нахождения коэффициентов ci

// Вычисление прогоночных коэффициентов (прямая прогонка)

Alpha[1] = 0;

Betta[1]  = 0;

for(i=1;i<=n-1;i++)

{

Alpha[i+1] = (-1)/(4+Alpha[i]);

Ti         = 3*(Yi[i+1]-2*Yi[i]+Yi[i-1])/(h*h) ;

Betta[i+1] = (Ti-Betta[i])/(4+Alpha[i]);

}

// Вычисление коэффициентов ci

// Обратная прогонка

Ci[n]=0;

for(i=n-1;i>=0;i--) { Ci[i] = Alpha[i+1]*Ci[i+1]+Betta[i+1]; }

// Находим коэффициенты bi,di

for(i=0;i<=n-1;i++)

{

Bi[i] = ((Yi[i+1]-Yi[i])/h)-(h*(Ci[i+1]+2*Ci[i])/3);

Di[i] = (Ci[i+1]-Ci[i])/(3*h);

}

Bi[n] = Bi[n-1]+2*Ci[n-1]*h+3*Di[n-1]*h*h;

Di[n] = Di[n-1];

printf("Значение функции f в точке x=%.2g равно %.4g\n",0.1,fn(0.1));

printf("Значение сплайна S в точке x=%.2g равно %.4g\n",0.1,Sx(0.1));

printf("Значение производной функции f' в точке x=%.2g равно

%.4g\n",0.1,fsh(0.1));

printf("Значение производной сплайна S' в точке x=%.2g равно

%.4g\n",0.1,Sshx(0.1));

getch();

}

Результаты работы программы

Значение функции f в точке x=0.1 равно 0.09983

Значение сплайна S в точке x=0.1 равно 0.09983

Значение производной функции f' в точке x=0.1 равно 0.995

Значение производной сплайна S' в точке x=0.1 равно 0.995