Если хотя бы одно из этих условий
не выполнено, то функция ![]() не
является линейным сплайном, если же они выполняются одновременно, то
не
является линейным сплайном, если же они выполняются одновременно, то ![]() является линейным сплайном. Проверим эти
условия. Первое условие выполнено, так как функции
является линейным сплайном. Проверим эти
условия. Первое условие выполнено, так как функции ![]() и
и ![]() являются полиномами первой степени. Второе
условие, при выполнении первого условия, достаточно проверить во внутренних
узлах сетки. В нашем случае только один внутренний узел сетки, а именно узел
являются полиномами первой степени. Второе
условие, при выполнении первого условия, достаточно проверить во внутренних
узлах сетки. В нашем случае только один внутренний узел сетки, а именно узел ![]() . Поэтому второе условие при выполнении
первого условия достаточно проверить только в точке
. Поэтому второе условие при выполнении
первого условия достаточно проверить только в точке ![]() , т.е. нужно проверить выполнение равенства
, т.е. нужно проверить выполнение равенства
![]() . Вычислим
. Вычислим ![]() и
и ![]() . Так как
. Так как ![]() , то
, то ![]() - непрерывная функция на отрезке
- непрерывная функция на отрезке ![]() . Оба условия выполнены, следовательно,
функция
. Оба условия выполнены, следовательно,
функция![]() является линейным
сплайном.
является линейным
сплайном.
Ответ: функция ![]() является линейным сплайном.
является линейным сплайном.
Задача 5. Определить,
является ли функция ![]() параболическим
сплайном, удовлетворяющим краевому условию
параболическим
сплайном, удовлетворяющим краевому условию ![]() , где
, где ![]() ,
,
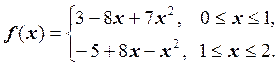
Решение.
Запишем функцию ![]() в виде:
в виде:
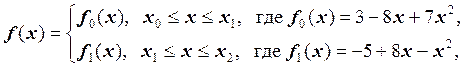
![]() ,
, ![]() ,
, ![]() . Для того, чтобы функция
. Для того, чтобы функция ![]() являлась параболическим сплайном,
удовлетворяющим краевому условию
являлась параболическим сплайном,
удовлетворяющим краевому условию ![]() ,
одновременно должны выполняться три условия:
,
одновременно должны выполняться три условия:
1. функции ![]() и
и ![]() - полиномы второй степени;
- полиномы второй степени;
2. функция ![]() - непрерывно дифференцируемая функция на
отрезке
- непрерывно дифференцируемая функция на
отрезке ![]() ;
;
3. функция ![]() удовлетворяет краевому условию
удовлетворяет краевому условию ![]() .
.
Если хотя бы одно из этих условий не выполнено, то функция ![]() не является параболическим сплайном,
удовлетворяющим заданному краевому условию. Проверим эти условия. Первое
условие выполнено, так как функции
не является параболическим сплайном,
удовлетворяющим заданному краевому условию. Проверим эти условия. Первое
условие выполнено, так как функции ![]() и
и ![]() являются полиномами второй степени. Второе
условие, при выполнении первого условия, достаточно проверить только во
внутренних узлах сетки. В нашем случае только один внутренний узел сетки, а
именно узел
являются полиномами второй степени. Второе
условие, при выполнении первого условия, достаточно проверить только во
внутренних узлах сетки. В нашем случае только один внутренний узел сетки, а
именно узел ![]() . Поэтому второе
условие, при выполнении первого условия, достаточно проверить только в точке
. Поэтому второе
условие, при выполнении первого условия, достаточно проверить только в точке ![]() , т.е. нужно проверить выполнение равенств
, т.е. нужно проверить выполнение равенств ![]() и
и ![]() . Вычислим
. Вычислим ![]() ,
, ![]() ;
;
![]() ,
, ![]() ,
, ![]() ,
, ![]() . Так как
. Так как ![]() , то
, то ![]() - непрерывно дифференцируемая функция на
отрезке
- непрерывно дифференцируемая функция на
отрезке ![]() . Для проверки третьего
условия вычислим значение производной функции
. Для проверки третьего
условия вычислим значение производной функции ![]() в точке
в точке ![]() :
: ![]() .
Так как
.
Так как ![]() , то третье условие
выполнено.
, то третье условие
выполнено.
Три условия выполняются одновременно, следовательно, функция ![]() является параболическим сплайном,
удовлетворяющим краевому условию
является параболическим сплайном,
удовлетворяющим краевому условию ![]() .
.
Ответ: функция ![]() является параболическим сплайном,
удовлетворяющим краевому условию
является параболическим сплайном,
удовлетворяющим краевому условию ![]() .
.
Задача 6. Определить является ли функция ![]() естественным кубическим сплайном, где:
естественным кубическим сплайном, где:
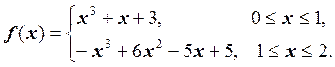
Решение. Запишем функцию ![]() в виде:
в виде:
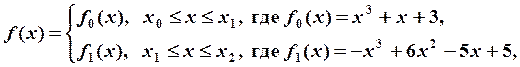
![]() ,
, ![]() ,
, ![]() . Для того, чтобы функция
. Для того, чтобы функция ![]() являлась естественным кубическим сплайном,
одновременно должны выполняться три условия:
являлась естественным кубическим сплайном,
одновременно должны выполняться три условия:
1. функции ![]() и
и ![]() - полиномы третьей степени;
- полиномы третьей степени;
2. функция ![]() - дважды непрерывно дифференцируемая
функция на отрезке
- дважды непрерывно дифференцируемая
функция на отрезке ![]() ;
;
3. функция ![]() удовлетворяет двум краевым условиям:
удовлетворяет двум краевым условиям: ![]() ,
,![]() .
.
Если хотя бы одно из этих условий не выполнено, то функция ![]() не является естественным кубическим
сплайном. Проверим эти условия. Первое условие выполнено, так как функции
не является естественным кубическим
сплайном. Проверим эти условия. Первое условие выполнено, так как функции ![]() и
и ![]() являются полиномами третьей степени.
Второе условие, при выполнении первого условия, достаточно проверить только во
внутренних узлах сетки. В нашем случае только один внутренний узел сетки, а
именно узел
являются полиномами третьей степени.
Второе условие, при выполнении первого условия, достаточно проверить только во
внутренних узлах сетки. В нашем случае только один внутренний узел сетки, а
именно узел ![]() . Поэтому второе
условие, при выполнении первого условия, достаточно проверить только в точке
. Поэтому второе
условие, при выполнении первого условия, достаточно проверить только в точке ![]() , т.е. нужно проверить выполнение равенств:
, т.е. нужно проверить выполнение равенств:
![]() ,
, ![]() и
и ![]() . Вычислим
. Вычислим ![]() ,
, ![]() ;
; ![]() ,
,
![]() ,
, ![]() ,
, ![]() ;
; ![]() ,
,
![]() ,
, ![]() ,
, ![]() . Так как
. Так как ![]() , то
, то ![]() - дважды непрерывно дифференцируемая
функция на отрезке
- дважды непрерывно дифференцируемая
функция на отрезке ![]() . Для проверки третьего
условия вычислим значения второй производной функции
. Для проверки третьего
условия вычислим значения второй производной функции ![]() в краевых точках:
в краевых точках: ![]() и
и ![]() . Третье условие выполнено.
. Третье условие выполнено.
Три условия выполняются
одновременно, следовательно, функция ![]() является
естественным кубическим сплайном.
является
естественным кубическим сплайном.
Построим алгоритм для
интерполяции функции ![]() на отрезке
на отрезке ![]() естественным интерполяционным кубическим
сплайном
естественным интерполяционным кубическим
сплайном ![]() с равномерным шагом. Будем опираться на
материал, изложенный в п.п.2.3.
с равномерным шагом. Будем опираться на
материал, изложенный в п.п.2.3.
Как и в задании 1, число
отрезков ![]() , шаг
, шаг![]() , где
, где ![]() ,
, ![]() . Введем
сетку на отрезке
. Введем
сетку на отрезке ![]() :
: ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.