Министерство образования и науки Российской Федерации
Комсомольский-на-Амуре государственный
технический университет
Методические указания к лабораторным работам по курсу
«Вычислительная математика» для студентов специальности 230105 и 010503
Комсомольск-на-Амуре 2005
Численные методы: Методические указания к лабораторным работам по курсу «Вычислительная математика» /Сост.: Н.Н. Михайлова, А.А. Хусаинов. Комсомольский – на – Амуре гос. техн. ун-т, 2005 – с.
Приводятся программа курса, задания к лабораторным работам, контрольные вопросы и задачи. Рассматриваются следующие темы: теория погрешностей, численные методы решения нелинейных уравнений, систем линейных уравнений и систем нелинейных уравнений, интерполяция функций, численное интегрирование и дифференцирование, численные методы решения задачи Коши для обыкновенных дифференциальных уравнений первого порядка.
Печатается по постановлению редакционно-издательского совета Комсомольского – на – Амуре государственного технического университета.
Рецензент Г.А. Леонтьева
Редакционно-издательский отдел Комсомольского – на – Амуре государственного технического университета
681013, Комсомольск – на – Амуре, пр. Ленина, 27.
Полиграфическая лаборатория Комсомольского – на – Амуре государственного технического университета
681013, Комсомольск – на – Амуре, пр. Ленина, 27.
1 Введение
Источники погрешности. Абсолютная и относительная погрешности. Верные знаки числа. Особенности математических вычислений, реализуемых на ЭВМ. Погрешность суммы, разности, произведения, частного, степени. Общая формула для погрешности.
3 Итерационные методы решения нелинейных уравнений
Отделение и уточнение корней. Метод простой итерации, теорема о сходимости, оценка погрешности. Метод Ньютона, метод хорд, комбинаторный метод хорд и касательных, метод итераций, оценка погрешности.
4 Прямые методы решения систем линейных уравнений
Векторные
и матричные нормы. Метод исключения неизвестных – Метод Гаусса. ![]() разложение матрицы. Метод Гаусса с
частичным выбором ведущего элемента (по столбцу). Метод Гаусса с полным выбором
ведущего элемента.
разложение матрицы. Метод Гаусса с
частичным выбором ведущего элемента (по столбцу). Метод Гаусса с полным выбором
ведущего элемента. ![]() разложение матрицы
разложение матрицы ![]() . Вектор невязки. Вычисление определителя,
нахождение обратной матрицы. Число обусловленности матрицы. Оценка возмущения
решения системы линейных уравнений при возмущении правой части.
. Вектор невязки. Вычисление определителя,
нахождение обратной матрицы. Число обусловленности матрицы. Оценка возмущения
решения системы линейных уравнений при возмущении правой части.
5 Итерационные методы решения систем линейных уравнений
Метод итераций, теорема о сходимости, оценка погрешности. Метод Зейделя.
6 Итерационные методы решения систем нелинейных уравнений
Отделение решения и уточнение решения. Метод итераций, теорема о сходимости. Метод Ньютона.
7 Интерполяция функций
Постановка задачи. Формула интерполяционного полинома Лагранжа и формула остаточного члена. Полиномы Чебышева и их свойства. Оптимальный выбор узлов интерполяции. Теорема Фабера. Конечные разности и разностные отношения. Интерполяционный полином Ньютона. Сплайн-интерполяция. Линейный сплайн, параболический сплайн. Кубический сплайн, оценка погрешности, нахождение коэффициентов кубического сплайна. Метод прогонки для решения систем линейных уравнений с трехдиагональными матрицами. Численное дифференцирование.
8 Численное интегрирование
Постановка задачи. Формула прямоугольников и формула остаточного члена. Формула трапеции и формула остаточного члена. Формула Симпсона и формула остаточного члена. Формула Эрмита. Численное интегрирование с неравномерным шагом. Экстраполяция по Ричардсону.
9 Численные методы решения задачи Коши для обыкновенных дифференциальных уравнений
Постановка задачи. Корректность и устойчивость задачи Коши. Метод сеток. Аппроксимация, устойчивость и сходимость. Метод Эйлера, метод Рунге-Кутта второго порядка, метод Рунге-Кутта четвертого порядка. Метод Милна. Численное решение задачи Коши для жестких уравнений.
Лабораторная работа 1
ИТЕРАЦИОННЫЕ МЕТОДЫ РЕШЕНИЯ НЕЛИНЕЙНЫХ УРАВНЕНИЙ.
Задание:
1) Отделить корни
уравнения ![]() графически и построить алгоритм
для уточнения одного из них комбинированным методом хорд и касательных с
точностью до
графически и построить алгоритм
для уточнения одного из них комбинированным методом хорд и касательных с
точностью до ![]() . Разработать программу, которая реализует
этот алгоритм и выдает на печать значение корня и значение функции
. Разработать программу, которая реализует
этот алгоритм и выдает на печать значение корня и значение функции ![]() в этой точке, а также строит график
функции
в этой точке, а также строит график
функции ![]() .
.
Варианты заданий
|
Номер варианта |
Уравнение |
Номер варианта |
Уравнение |
|
1 |
|
16 |
|
|
2 |
|
17 |
|
|
3 |
|
18 |
|
|
4 |
|
19 |
|
|
5 |
|
20 |
|
|
6 |
|
21 |
|
|
7 |
|
22 |
|
|
8 |
|
23 |
|
|
9 |
|
24 |
|
|
10 |
|
25 |
|
|
11 |
|
26 |
|
|
12 |
|
27 |
|
|
13 |
|
28 |
|
|
14 |
|
29 |
|
|
15 |
|
30 |
|
Контрольные вопросы:
1) Метод простой итерации.
2) Метод Ньютона.
3) Метод хорд.
4) Комбинированный метод хорд и касательных.
5) Метод итераций.
Пояснение: Ответ на
каждый из этих вопросов включает в себя условия на функцию ![]() , при выполнении которых возможно
применение метода, выбор начального приближения, формулу метода, условие сходимости,
условие остановки итерационного процесса.
, при выполнении которых возможно
применение метода, выбор начального приближения, формулу метода, условие сходимости,
условие остановки итерационного процесса.
Задачи к лабораторной работе 1
1) Число ![]() содержит
содержит ![]() верных знаков, определить какова относительная
погрешность этого числа.
верных знаков, определить какова относительная
погрешность этого числа.
2) Определить
сколько верных знаков содержит число ![]() , если относительная
погрешность этого числа составляет 5%.
, если относительная
погрешность этого числа составляет 5%.
3) Заданы числа ![]() и
и ![]() с
абсолютными погрешностями
с
абсолютными погрешностями ![]() и
и ![]() . Найти относительные погрешности суммы,
разности, частного и произведения этих чисел.
. Найти относительные погрешности суммы,
разности, частного и произведения этих чисел.
4) Найти абсолютную
и относительную погрешности вычисления значения функции ![]() .
.
5) Построить и обосновать алгоритм для вычисления с точностью
![]()
а) по методу Ньютона;
б) по методу хорд;
в) по методу итераций;
г) по комбинированному методу хорд и касательных.
6) Отделить корни
уравнения ![]() и построить алгоритм для уточнения одного
из них с точностью до
и построить алгоритм для уточнения одного
из них с точностью до ![]()
а) методом Ньютона;
б) методом хорд;
в) методом итераций;
г) комбинированным методом хорд и касательных;
д) методом простой итерации.
Лабораторная работа 2
РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ
Задание:
1) Разработать
программу, которая, используя метод Гаусса с частичным выбором ведущего
элемента, решает систему линейных уравнений ![]() ,
находит определитель матрицы
,
находит определитель матрицы ![]() , вычисляет вектор невязки.
, вычисляет вектор невязки.
Варианты заданий
1. 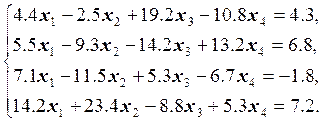 2.
2. 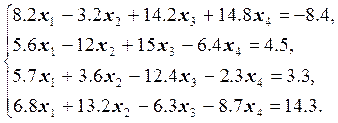
3. 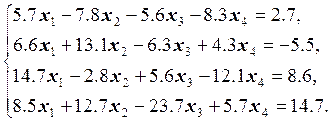 4.
4. 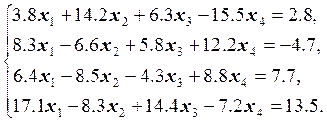
5. 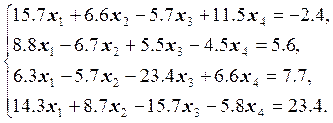 6.
6. 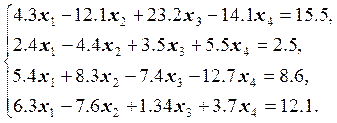
7. 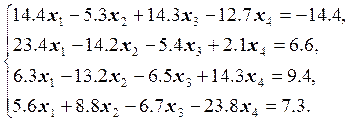 8.
8. 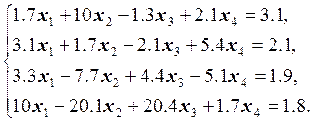
9. 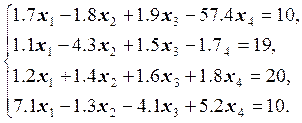 10.
10. 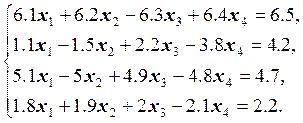
11. 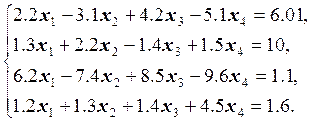 12.
12. 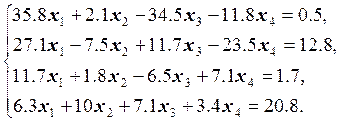
13. 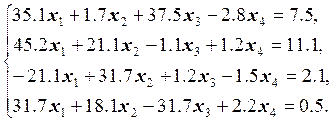 14.
14. 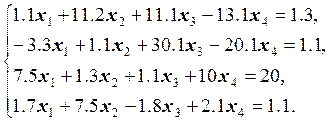
15. 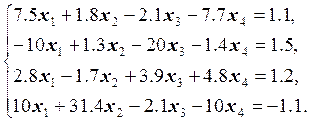 16.
16. 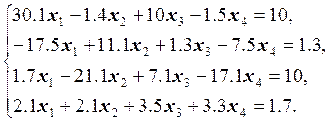
17. 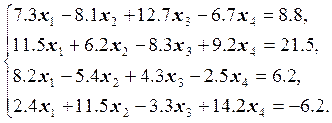 18.
18. 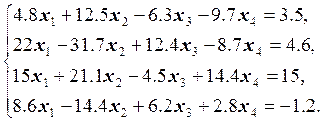
19. 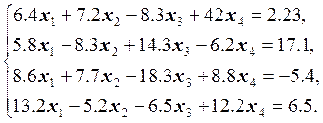 20.
20. 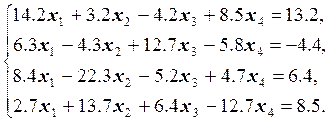
21. 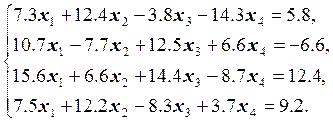 22.
22. 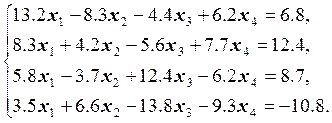
23. 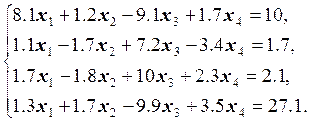 24.
24. 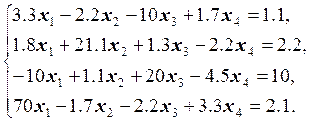
25. 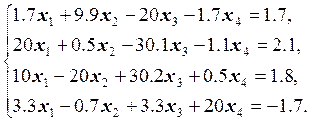 26.
26. 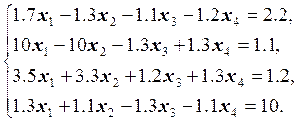
27. 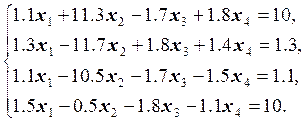 28.
28. 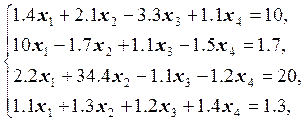
29. 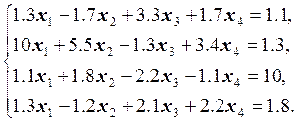 30.
30. 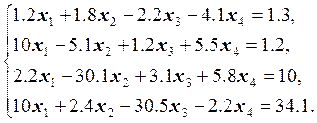
2) Построить
алгоритм для решения системы линейных уравнений методом итераций с точностью до
![]() и оценить число шагов, необходимых для
достижения точности
и оценить число шагов, необходимых для
достижения точности ![]()
Варианты задания 2
|
№ |
СЛУ |
№ |
СЛУ |
№ |
СЛУ |
|
|
0.82x+0.04y–0.17z =1.42, 0.15x+1.24y+0.03z =-1.83, 0.11x-0.04y+0.85z =0.43. |
11 |
0.91x-0.18y+0.14z =1.17, 0.14x+1.19y+0.07z =2.15, 0.12x-0.02y+0.87z =0.42. |
21 |
0.93x-0.14y+0.11z =2.17, 0.11x+1.23y-0.15z =-8.31, 0.12x-0.13y+0.94z =0.18. |
|
|
0.91x-0.03y+0.07z =-2.14, 0.02x+1.13y-0.11z =1.45, 0.07x+0.14y+0.82z =0.14. |
12 |
0.93x-0.04y+0.12z =2.18, 0.15x+1.25y-0.03z =1.41, 0.09x-0.12y+0.87z =2.41. |
22 |
0.89x-0.15y–0.14z =0.19, 0.13x+1.25y+0.11z =-5.41, 0.12x-0.14y+0.92z =2.37. |
|
3 |
0.88x-0.12y+0.05z =2.43, 0.14x+0.92y-0.13z =1.15, 0.16x-0.03y+1.25z =2.03. |
13 |
0.92x-0.11y+0.17z =2.83, 0.13x+1.18y-0.08z =1.48, 0.12x-0.14y+0.91z =-1.46. |
23 |
0.89x-0.18y+0.05z =2.41, 0.11x+0.93y-0.14z =-5.48, 0.12x-0.13y+1.18z =0.14. |
|
4 |
0.93x-0.04y+0.13z =1.23, 0.15x+1.17y-0.08z =-2.15, 0.13x-0.18y+0.89z =0.52. |
14 |
0.89x+0.12y–0.09z =5.41, 0.11x+0.93y-0.15z =-1.18, 0.03x-0.17y+1.23z =-3.15. |
24 |
0.95x+0.18y–0.13z =0.13, 0.12x+1.15y-0.18z =-1.18, 0.13x-0.19y+1.22z =6.41. |
|
|
0.87x-0.04y+0.14z =2.41, 0.13x+1.28y+0.04z =1.48, 0.12x-0.17y+0.93z =-2.65. |
15 |
1.15x-0.12y+0.03z =1.19, 0.03x+1.09y-0.09z =2.18, 0.04x-0.21y+0.94z =-5.18. |
25 |
0.84x-0.18y+0.14z =5.41, 0.14x+1.04y-0.15z =-6.81, 0.12x-0.13y+0.96z =2.38. |
|
|
0.89x-0.11y+0.04z =-1.21, 0.11x+1.21y+0.13z =0.23, 0.03x-0.12y+0.97z =1.42. |
16 |
0.87x+0.12y–0.14z =3.18, 0.07x+0.92y-0.14z =0.09, 0.11x-0.18y+1.15z =-4.08. |
26 |
0.92x-0.15y+0.18z =0.71, 0.13x+1.23y-0.14z =0.21, 0.12x-0.21y+1.05z =-5.41. |
|
7 |
0.93x-0.02y–0.16z =1.15, 0.03x+1.27y-0.11z =-2.13, 0.04x-0.18y+0.92z =1.84. |
17 |
0.92x-0.12y+0.03z =0.18, 0.11x+1.24y-0.15z =-2.81, 0.03x-0.12y+0.93z =2.31. |
27 |
0.91x-0.21y+0.18z =-0.15, 0.13x+1.27y-0.07z =-2.41, 0.11x-0.19y+1.14z =5.43. |
|
8 |
0.83x-0.11y+0.04z =0.63, 0.12x+1.18y-0.13z =-1.48, 0.04x-0.13y+0.88z =0.41. |
18 |
0.87x-0.11y+0.13z =2.15, 0.13x+1.15y-0.18z =-4.18, 0.11x-0.14y+0.91z =2.11. |
28 |
0.88x-0.15y+0.13z =2.31, 0.19x+1.23y-0.08z =-4.15, 0.09x-0.15y+0.92z =-5.81. |
|
9 |
0.84x-0.13y+0.04z =-1.84, 0.06x+0.92y-0.13z =0.42, 0.04x+0.11y+1.12z =0.18. |
19 |
0.91x-0.11y+0.14z =3.14, 0.11x+1.21y-0.14z =0.13, 0.14x-0.12y+0.91z =-4.18. |
29 |
0.92x-0.12y+0.18z =4.15, 0.14x+1.21y-0.13z =-0.18, 0.11x-0.18y+1.08z =0.12. |
|
10 |
0.83x-0.11y+0.08z =-1.14, 0.04x+1.12y-0.11z =2.41, 0.13x-0.17y+1.14z =2.15. |
20 |
0.92x-0.13y+0.18z =2.13, 0.12x+1.19y-0.13z =0.81, 0.11x-0.13y+1.21z =2.43. |
30 |
0.94x-0.11y+0.21z =2.18, 0.15x+1.24y-0.07z =0.18, 0.13x-0.19y+1.08z =-5.78. |
Контрольные вопросы:
1) Идея метода Гаусса. Метод Гаусса без выбора ведущего элемента, метод Гаусса с частичных выбором ведущего элемента, метод Гаусса с полным выбором ведущего элемента.
2) Вычисление определителя матрицы и нахождение обратной матрицы методом Гаусса.
3) Определение вектора невязки.
4) Метод итераций
для решения систем линейных уравнений, условие сходимости, оценки погрешности,
оценка числа шагов, необходимых для достижения точности ![]() ,
условие остановки итерационного процесса.
,
условие остановки итерационного процесса.
Задачи к лабораторной работе 2
1) Построить ![]() разложение матрицы
разложение матрицы ![]() .
.
2) Решить систему линейных уравнений методом Гаусса без выбора ведущего элемента, с частичным выбором ведущего элемента, с полным выбором ведущего элемента.
3) Построить и
обосновать алгоритм решения системы линейных уравнений методом итераций.
Оценить число шагов, необходимых для достижения точности ![]() .
.
4) С помощью метода Гаусса определить, имеет ли решение система линейных уравнений.
5) Заданы две системы линейных уравнений с одинаковыми матрицами и близкими правыми частями. Найти решения этих систем линейных уравнений и объяснить полученный результат.
Лабораторная работа 3
ИТЕРАЦИОННЫЕ МЕТОДЫ РЕШЕНИЯ СИСТЕМ НЕЛИНЕЙНЫХ УРАВНЕНИЙ
Задание:
1) Отделить решение
системы нелинейных уравнений и построить алгоритмы для уточнения решения
методом итераций и методом Ньютона с точностью до ![]() .
Разработать программу которая реализует эти алгоритмы и выдает на печать
полученные решения.
.
Разработать программу которая реализует эти алгоритмы и выдает на печать
полученные решения.
1. 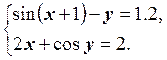 2.
2. 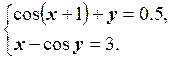 3.
3. 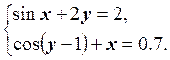
4. 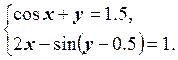 5.
5. 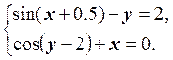 6.
6. 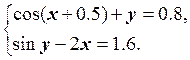
7. 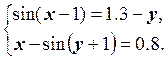 8.
8. 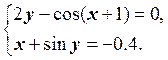 9.
9. 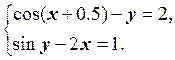
10. 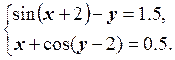 11.
11. 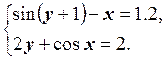 12.
12. 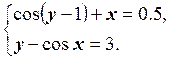
13. 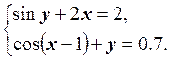 14.
14. 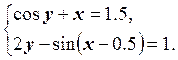 15.
15. 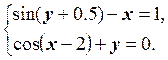
16. 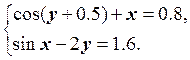 17.
17. 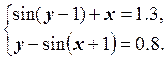 18.
18.
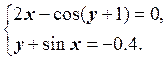
19. 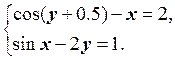 20.
20. 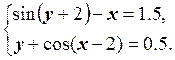 21.
21. 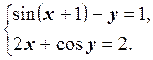
22. 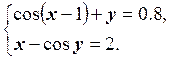 23.
23. 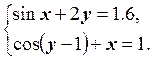 24
24 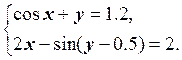
25. 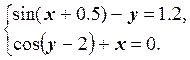 26.
26. 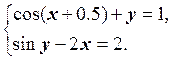 27.
27. 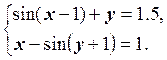
28.
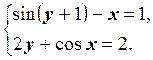 29.
29. 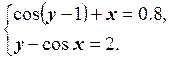 30.
30. 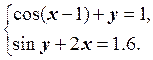
Контрольные вопросы:
1) Метод итераций для решения систем нелинейных уравнений.
2) Метод Ньютона для решения систем нелинейных уравнений.
Задачи к лабораторной работе 3
1) Известно, что
решение системы нелинейных уравнений принадлежит области ![]() . Построить и обосновать алгоритмы решения
системы методом итераций и методом Ньютона с точностью до
. Построить и обосновать алгоритмы решения
системы методом итераций и методом Ньютона с точностью до ![]() .
.
2) Отделить решение
системы нелинейных уравнений. Построить и обосновать алгоритм решения системы
нелинейных уравнений методом Ньютона и методом итераций с точностью до ![]() .
.
Лабораторная работа 4
Задание:
1) По формуле функции f(x) на интервале [-1,1] построить интерполяционные таблицы с равномерным шагом для числа точек n1 и n2. Построить интерполяционные полиномы g1(x) и g2(x) для числа точек n1 и n2. Для контроля распечатать интерполяционные таблицы и значения интерполяционных полиномов g1(x) и g2(x) в узлах интерполяции. Для K=l00 построить графики функции f(x) и интерполяционных
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.