

































Дифференциальными уравнениями называются такие уравнения, в которых функции одного или нескольких переменных причем в уравнения входят не только функции но и производные.
Если функции одного переменного то такие дифференциальные уравнения – обыкновенные дифференциальные уравнения.
Порядком дифференциального уравнения называется максимальный порядок производной или дифференциала от неизвестной функции.
В общем виде записывается:
![]()
![]() - аргумент
- аргумент
![]() -
функция
-
функция
![]() -
производная
-
производная
Функция ![]() может
быть определена не на всей области значения своих переменных а на некоторой
области
может
быть определена не на всей области значения своих переменных а на некоторой
области ![]() .
.
Решением уравнения называется такая функция ![]() определенна на интервале
определенна на интервале ![]() , которая при подстановке в дает тождество на всем интервале
, которая при подстановке в дает тождество на всем интервале ![]() .
.
Интервал ![]() называется
интервалом определения решения и обозначается
называется
интервалом определения решения и обозначается ![]() .
.
Подставляя ![]() в мы предполагаем что существует
в мы предполагаем что существует ![]() , то есть что
, то есть что ![]() непрерывна.
непрерывна.
Кроме того необходимо чтобы
выполнялось условие ![]() .
.
Решение (интеграл) содержащее число произвольных постоянных равное порядку дифференциального
уравнения называется общим решением и имеет вид ![]() , где С
– произвольные постоянные.
, где С
– произвольные постоянные.
Выбрав некоторое значение С получаем частное решение дифференциального уравнения.
Решение дифференциального уравнения можно считать найденным если оно представлено в виде выражения содержащее квадратуры, для которых интеграл может быть выражен в виде элементарных функциях либо подсчитан приблизительно.
Правильность полученного решения проверяется подстановкой.
Если дифференциальное уравнение имеет вид
![]() то оно называется уравнением разрешимым относительно
производной.
то оно называется уравнением разрешимым относительно
производной.
Если можно записать дифференциал
![]() , то
, то ![]()
![]()
Пусть на плоскости ![]() задана функция
задана функция ![]() -
правая часть .
-
правая часть . ![]() может быть определена не на всей
плоскости, а на области Г(открытое множество).
может быть определена не на всей
плоскости, а на области Г(открытое множество).
Пусть ![]() и
и
![]() - непрерывные функции заданные на Г.
- непрерывные функции заданные на Г.
Решение ![]() представимо
в виде некоторой кривой.
представимо
в виде некоторой кривой.
Общее решение известно с точностью до константы С, то есть все возможные частные решения образуют семейство кривых.
![]() -
интегральная кривая дифференциального уравнения .
-
интегральная кривая дифференциального уравнения .
Уравнение устанавливает зависимость между ![]() и угловым
коэффициентом касательной к графику решения в этой точке. Зная
и угловым
коэффициентом касательной к графику решения в этой точке. Зная ![]() мы можем вычислить
мы можем вычислить ![]() и
решить . Дифференциальное уравнение определяет поле направлений. Тогда задачей интегрирования дифференциального уравнения будет определение
интегральных кривых направление касательных к которым в каждой точке совпадает
с направлением поля.
и
решить . Дифференциальное уравнение определяет поле направлений. Тогда задачей интегрирования дифференциального уравнения будет определение
интегральных кривых направление касательных к которым в каждой точке совпадает
с направлением поля.
Пример
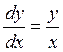
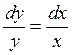
В каждой точке кроме (0,0)
угловой коэффициент касательной к искомой кривой равен отношению ![]() т.е он совпадает с угловым коэффициентом
кривой направленным из начала координат в точку
т.е он совпадает с угловым коэффициентом
кривой направленным из начала координат в точку ![]() . Для
такого поля направлений интегральные кривые будут иметь вид
. Для
такого поля направлений интегральные кривые будут иметь вид ![]() .
.
![]() уравнение с разделяемыми переменными. Функции Ошибка!
Объект не может быть создан из кодов полей редактирования. предполагаются
непрерывными.
уравнение с разделяемыми переменными. Функции Ошибка!
Объект не может быть создан из кодов полей редактирования. предполагаются
непрерывными.
Пусть ![]() -
решение т.е. подставляя
-
решение т.е. подставляя ![]() в получим тожество, проинтегрировав которое мы получим соотношение определяющее решение
в получим тожество, проинтегрировав которое мы получим соотношение определяющее решение
![]()
Соотношению будет удовлетворять каждое решение , в свою очередь интегральное соотношение будет удовлетворять дифференциальному уравнению . ![]() определяющая
определяющая ![]() называется
общим интегралом данного уравнения. Получить частное решение можно, задав
значение
называется
общим интегралом данного уравнения. Получить частное решение можно, задав
значение ![]() .
.
![]() - уравнение
такого вида, в котором коэффициенты перед дифференциалом распадаются на функции
зависящие от различных переменных называются уравнениями с разделяющимися
коэффициентами.
- уравнение
такого вида, в котором коэффициенты перед дифференциалом распадаются на функции
зависящие от различных переменных называются уравнениями с разделяющимися
коэффициентами.
Разделим обе части этого
уравнения на ![]() получим:
получим:
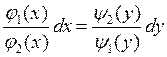 - уравнения с разделенными коэффициентами.
- уравнения с разделенными коэффициентами.
Деление на ![]() может привести к потере решений. (Не
забывать выписывать частные решения). Если
может привести к потере решений. (Не
забывать выписывать частные решения). Если ![]() разрывные
то появятся лишние решения, которые обращают в ноль дробь
разрывные
то появятся лишние решения, которые обращают в ноль дробь 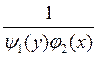 .
.
1) ![]()
Уравнение такого типа решается
заменой: ![]()
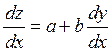 т.е.
т.е. ![]() .
. 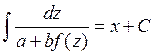
Уравнение называется однородным
если функция ![]() однородна относительно
однородна относительно ![]() если при замене
если при замене ![]() на
на
![]() мы получим
мы получим ![]() . k – степень однородности.
. k – степень однородности.
2) Уравнения приводящиеся к однородным.
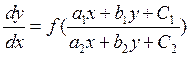
Для решение данного уравнения необходимо преобразовать это уравнения путем переноса начала координат в точку пересечения кривых.
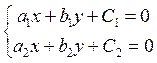 =>
=> ![]()
![]() ,
, ![]()
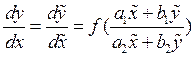 =>
=>
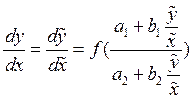
Если исходные прямые параллельны, то исходное уравнение можно переписать:
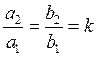
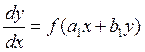
3) Линейное уравнение первого порядка.
![]()
![]() -
непрерывные функции. Если
-
непрерывные функции. Если ![]() то уравнение
то уравнение ![]() называется однородным линейным уравнением.
называется однородным линейным уравнением.
Для решения уравнения необходимо решить соответствующее ему однородное уравнение.
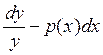
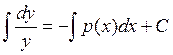
![]()
![]()
Получив решение однородного
уравнения, воспользуемся методом вариации постоянных. Пусть![]() , тогда
, тогда ![]() (*).
Подставим (*) в :
(*).
Подставим (*) в :
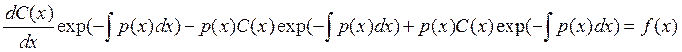 =>
=>
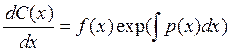
![]()
В общем виде решение будет иметь вид: ![]()
4) Уравнение Бернулли.
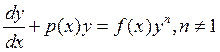
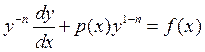 Сделаем
замену:
Сделаем
замену: ![]()
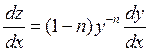
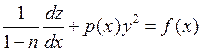
5)Уравнение Риккати
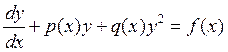
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.