Дифференциальные уравнения первого порядка, страница 6

ЛЕММА:

Пусть даны два линейных однородных уравнения n-го порядка

                                

                                 

И пусть , с непрерывными коэффициентами p_i(x) b q_i(x) имеют общие фундаментальные системы решений. ФСР – л.н.з. частные решения однородного уравнения (3).

Если уравнения (6),(7) q_i(x)=p_i(x) , .

На основании леммы можно сделать ВЫВОД, что ФСР определяет ДУ (1), т.е. по имеющему ФСР можно восстановить ДУ (1).

Найдем вид (1) имеющему ФСР y₁,y₂,…,y_n. По теореме (2) любое решение y(x) уравнения (1) линейно зависит от ФСР, а это значит если в общем виде записать W[y₁,y₂,…,y_n,y] определитель Вронского для системы y₁,y₂,…,y_n,y

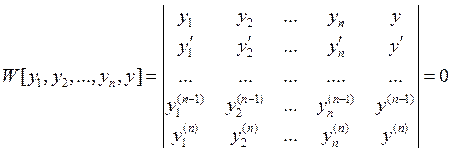 , т.к  y л.з. от

Раскладывая определитель Вронского по последней строчке мы получим:

p(x)0, значит можно разделить правую и левую часть уравнения и получится уравнение вида (1) с коэффициентами

                (*)

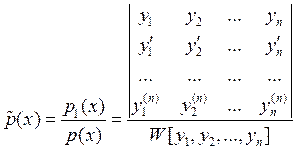
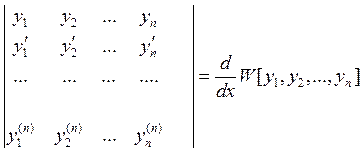По правилу дифференцирования определителя (производная от определителя равна определителей i строка каждого из которых равна производной от i строки исходного определителя). Если (4) продифференцировать

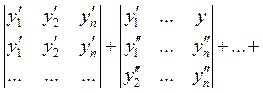
0                       0

т.е. от этой суммы останется только последний i, а он есть определитель из соотношения (*)

                                            

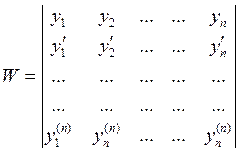
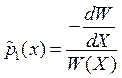
Если известны начальные условия получаем

                                        

Формулы , называется формулами Остроградского – Лиувилля. Эти соотношения можно использовать интегрирования линейного однородного уравнения 2 – го порядка.

Пусть нам известно одно из частных решений y₁(x)

                                      

Согласно , любое решение уравнения должны удовлетворять следующему соотношению

                               

Линейные однородные уравнения с постоянными коэффициентами

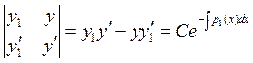
Пусть дано уравнение вида

                                   

                                                   

Частные решения могут быть определены в виде . Подставим  в и получим

                                      

И все решения уравнения определяется типом корней характеристического уравнения .

1)  Все  и различны

2)  Если все , а корни  для него существует комплексно сопряженное , тогда согласно теореме о частных решениях одного уравнения с вещественным оператором имеющим комплексное решение. Действительная и мнимая часть решений

будут решением , т.е.

3)  Если корень k имеет кратность , тогда частные решения уравнения будут иметь вид:.

Предположим, что . Если подставим корни в характеристическое уравнение, то мы получим , тогда получаем

                                   ему будет соответствовать ДУ

                                 

Частные решения этого уравнения будут полиномами степени <

                                               

Пусть . Сделаем замену

                                                    

Подставим в и получим уравнение однородное относительно . Это будет уравнение n-го порядка с постоянными коэффициентами:

                                                         

Корни  характеристического уравнения отличны от корней характеристического уравнения на соответствующее слагаемое .

,  – корни характеристического уравнения . Если , тогда , Соответственно если корни нулевые, то частные решения ДУ определяется формулой . Тогда частные решения будут иметь вид:

                                      

Общее решение будет линейная комбинация этих решений:

 

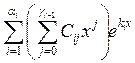
 – количество различных собственных значений.

 – кратность каждого из собственных значений.

Уравнения Эйлера

Уравнение вида ,  – называется уравнением Эйлера. Это уравнение заменой сводится к уравнению с постоянными коэффициентами. Можно не делать замены переменных, а сразу искать решение в виде , тогда частные решения будут иметь вид:

Линейные неоднородные уравнения

                                 

Если в , то делим на