Дифференциальные уравнения первого порядка, страница 10

Т1. ОСЛДУ устойчива тогда и только тогда, когда каждое решение  этой системы ограничено на множестве .

Следствие. Если НСЛДУ (1) устойчива, то все ее решения одновременно ограничены или одновременно неограниченны при .

Т2. ОСЛДУ асимптотически устойчива тогда, когда для всех ее решений:  

Следствие. Асимптотически устойчивая ЛСДУ асимптотически устойчива в целом.

Устойчивость линейной системы ДУ с постоянной матрицей.

Пусть дана система 

                                                 

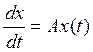
Тогда решение можно искать в виде:  

U- некоторый вектор. Подставим в ур-ие:

                                                 

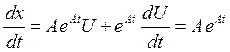
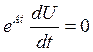
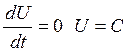
Решение будет иметь вид:

                                                   

                                                  

Пусть дано начальное условие. Тогда из получим

, 

                                                  и решение

                                                 

Пусть   - собственные значения,

- размерность соответствующих клеток Жордана.

 - соответствующая клетка Жордана.

  

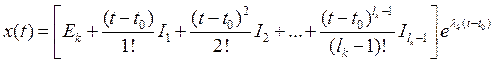
 - косые матрицы( функции от Жордановой формы)

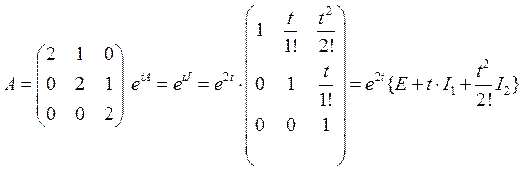
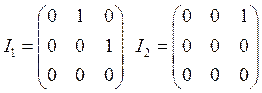
Т. ЛОСДУ с постоянной матрицей устойчива тогда и только тогда, когда все с.з. матрицы А обладают неположительной действительной частью. Причем, те с.з., у которых действительная часть рана 0, допускают лишь простые элементарные делители, т.е. им соответствует Жорданова клетка размерностью 1.

Док-во:

Необходимость: Пусть  

И соответственно  - их р штук и им соответствует р Жордановых клеток, размерностью  .

И  (нулевая действительная часть),

     

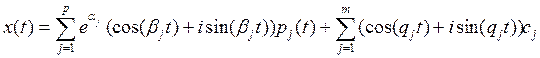
– однородное решение

  - некоторые полиномиальные векторы функции

  - некоторые постоянные векторы-столбцы.

Степень  на 1 меньше порядка соответствующей Жордановой клетки 

, значит , значит решение x(t) – ограничено, т.е. , значит оно устойчиво.

Достаточность: Пусть система устойчива. Сначала покажем, что все с.з. матрицы А неположительные (все ).

Пусть есть  . Ему будет соответствовать  . И   - противоречие, значит  .

Теперь покажем, что если  , тогда этому с.з. соответствует простой элементарный делитель.

Если  , то некоторое частное решение, соответствующее одной Жордановой клетке, будет иметь вид:   - частное решение .

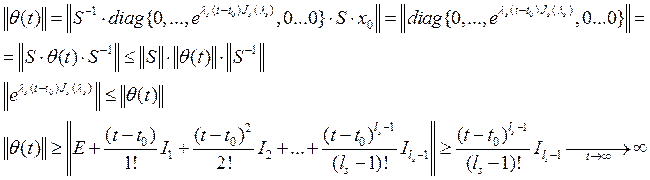
норма неограниченна. Это невозможно, т.к. система устойчива. Значит,   - простые элементарные делители.

Замечание. Устойчивая ОСЛДУ с постоянной матрицей А равномерно устойчива относительно начального условия .

Т. ОСЛДУ с постоянной матрицей асимптотически устойчива, когда все с.з. матрицы А имеют отрицательные действительные части.

Точки покоя.

О.

                                          

Если эта система имеет решение , то траектория этого решения сходится в n-мерном пространстве в точке  и эта точка называется точкой покоя для данной системы ДУ.

Если интерпретировать решение ДУ, как траекторию в N-мерном пространстве, зависящую от параметра t (времени), тогда решение системы, состоящее из const, будет точкой покоя данной системы. Тривиальное решение – это тоже точка покоя.

Типы точек покоя.

1. если с.з. действительны и различны

1.

точка покоя (т.п.) называется устойчивым узлом. Все  будут стягиваться в т.п.

2.

т.п. называется неустойчивым узлом. С ростом t все траектории будут удаляться от т.п.

3.

т.п. называется седлом (неустойчивая).

2. если с.з. комплексные

1.  

т.п. называется устойчивым фокусом.

2.  

т.п. называется неустойчивым фокусом.

3.

т.п. называется центром (устойчивая).

3.  - с.з. кратные

1.  

т.п. асимптотически устойчива (устойчивый узел).

2.  

т.п. называется неустойчивым узлом.

Второй метод Ляпунова.

Пусть дана система ДУ . Будем исследовать на устойчивость тривиальное решение  . Если с ростом  точки всех траекторий будут приближаться к т.п. или хотя бы не удаляться от начала координат, то исследуемая т.п. – устойчивая.

- расстояние от точки  до начала координат.