Краевые задачи определяют поведение функции и (или) ее производных на границе области. К краевым задачам относится задача о стационарном распространении тепла в стержне, на концах может быть задана постоянная температура, тогда эта задача будет иметь вид:
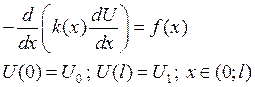 ,
, ![]()
где ![]() ,
, ![]() ,
, ![]() .
.
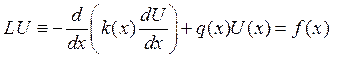
![]()
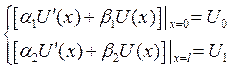
![]() , где
, где ![]() - заданные числа, одновременно не равные
0.
- заданные числа, одновременно не равные
0.
Если в 3 ![]() , то получим краевые
условия первого рода или условия Дирихле.
, то получим краевые
условия первого рода или условия Дирихле.
Если в 3 ![]() , то получим краевые
условия второго рода или условия Неймана.
, то получим краевые
условия второго рода или условия Неймана.
Если в 3 ![]() , то краевые условия
третьего рода или смешанные краевые условия.
, то краевые условия
третьего рода или смешанные краевые условия.
Однородной краевой задачей называется задача 2, 3 при
![]() ,
, ![]() .
.
Однородная краевая задача всегда имеет тривиальное решение, но может существовать и нетривиальное решение. Частным случаем однородной краевой задачи является задача на собственные значения. Она состоит в определении значений параметров, входящих в ДУ при которых существует нетривиальное решение однородных задач:

![]() , где L – линейный диф. оператор, например из 2.
, где L – линейный диф. оператор, например из 2. ![]() - заданная функция (непрерывная и
интегрируемая на
- заданная функция (непрерывная и
интегрируемая на ![]() ),
), ![]() -
заданные числа.
-
заданные числа.
Значения параметра ![]() , при
котором задача 4 имеет нетривиальное решение, называется собственными
значениями, а соотв. им нетривиальные решения – собственными функциями
данной краевой задачи.
, при
котором задача 4 имеет нетривиальное решение, называется собственными
значениями, а соотв. им нетривиальные решения – собственными функциями
данной краевой задачи.
Задача 4 – это и есть задача Штурма-Лиувилля.
Собственные значения 4 обладают свойствами:
Теорема о разложимости Стеклова.
Если функция ![]() дважды непрерывно дифференцируема, т.е.
дважды непрерывно дифференцируема, т.е. ![]() на
на ![]() , и
удовлетворяет соотв. однородным краевым условиям 4, то ее можно представить в
виде абсолютно и равномерно сходящегося ряда на
, и
удовлетворяет соотв. однородным краевым условиям 4, то ее можно представить в
виде абсолютно и равномерно сходящегося ряда на ![]() по
собственным функциям
по
собственным функциям ![]() задачи 4, т.е.
задачи 4, т.е.
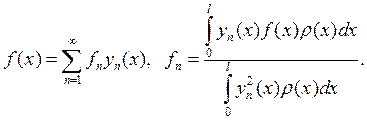
Пример:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
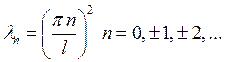
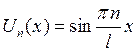
Пусть дано 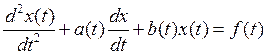
![]() с однородными краевыми условиями
с однородными краевыми условиями 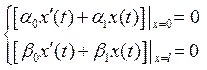
![]() и
и ![]() и
и ![]() . И
пусть данная краевая задача имеет единственное решение. Рассмотрим однородное
уравнение
. И
пусть данная краевая задача имеет единственное решение. Рассмотрим однородное
уравнение 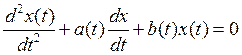 .
. ![]()
Пусть ![]() - решение однородного
уравнения 3, удовлетворяющее краевому условию 2.1. А решение
- решение однородного
уравнения 3, удовлетворяющее краевому условию 2.1. А решение ![]() удовлетворяет 3 и краевому условию 2.2.
Тогда по построению
удовлетворяет 3 и краевому условию 2.2.
Тогда по построению ![]() не должно удовлетворять 2.2, а
не должно удовлетворять 2.2, а ![]() не должно удовлетворять 2.1. Если бы было
не так, то
не должно удовлетворять 2.1. Если бы было
не так, то ![]() и
и ![]() были бы
зависимы, что нас не интересует, и противоречило бы предположению о
единственности решения (т.к.
были бы
зависимы, что нас не интересует, и противоречило бы предположению о
единственности решения (т.к. ![]() является решением 2,3 и
их было бы бесконечно много).
является решением 2,3 и
их было бы бесконечно много).

![]()
Решения ![]() и
и ![]() линейно независимы. Можем искать решение
неоднородной задачи методом вариации постоянных:
линейно независимы. Можем искать решение
неоднородной задачи методом вариации постоянных: ![]() .
. ![]()
![]() и
и ![]() должны
удовлетворять условию
должны
удовлетворять условию 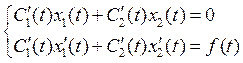 .
.
Из-за линейной независимости 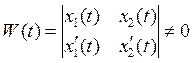 ;
;
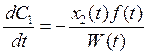
![]() и
и 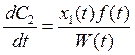
![]()
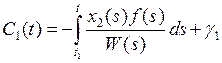 и
и  .
.
Подставим ![]() и
и ![]() в соотношение 5. Получим
в соотношение 5. Получим
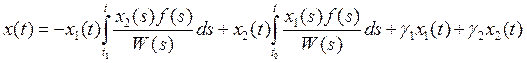
![]()
Подставим 8 в краевое условие 2. Получим
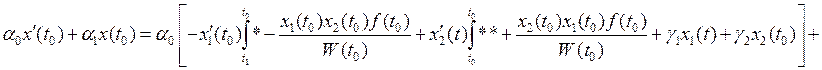
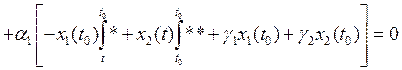 . При этом
. При этом ![]() удовлетворяет 2.1.
удовлетворяет 2.1.
После приведения подобных, получим ![]() .
С учетом того, что
.
С учетом того, что ![]() и
и ![]() , то 8
можно переписать в виде
, то 8
можно переписать в виде 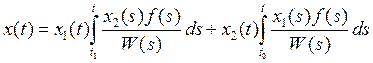 .
. ![]()
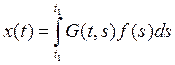
![]() , где
, где 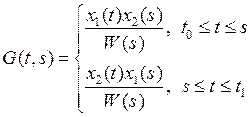
![]()
Функция ![]() называется функцией
Грина для краевой задачи 1,2. И если функция Грина построена, то решение
краевой задачи 1,2 определяется формулой 10. Сама функция Грина строится только
по линейно независимым решениям
называется функцией
Грина для краевой задачи 1,2. И если функция Грина построена, то решение
краевой задачи 1,2 определяется формулой 10. Сама функция Грина строится только
по линейно независимым решениям ![]() и
и ![]() , и от правой части
, и от правой части ![]() не
зависит. При фиксированном
не
зависит. При фиксированном ![]() функция Грина обладает
следующими свойствами:
функция Грина обладает
следующими свойствами:
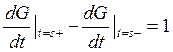 (функция Грина – отклик системы на
единичное возмущение).
(функция Грина – отклик системы на
единичное возмущение).Пример:
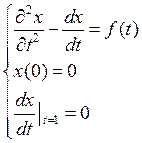
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

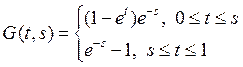
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.