Перепишем в виде
![]()
С помощью замены переменных ![]() можно свести процесс поиска решения в
окрестности к поиску решения в окрестности точки
можно свести процесс поиска решения в
окрестности к поиску решения в окрестности точки ![]() . В
дальнейшем будем рассматривать решение в точке
. В
дальнейшем будем рассматривать решение в точке ![]() .
.
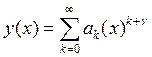
При подстановке в получим соотношения для ![]() . Первые 1 или 2 соотношения
позволяют вычислить
. Первые 1 или 2 соотношения
позволяют вычислить ![]() и называются определяющими.
и называются определяющими.
Теорема Фукса:
Пусть дано диф.
уравнение такое, что функции ![]() и
и ![]() имеют
полюсы (точка, в которой функция терпит разрыв) в точке
имеют
полюсы (точка, в которой функция терпит разрыв) в точке ![]() .
Тогда решение можно искать в виде при условии, что будут конечны произведения
.
Тогда решение можно искать в виде при условии, что будут конечны произведения ![]() ,
,![]()
Пусть дано и функции ![]() и
и ![]() условиям
теоремы Фукса:
условиям
теоремы Фукса:
![]()
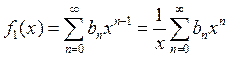
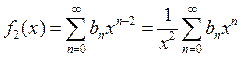
Подставим (5) в (4):
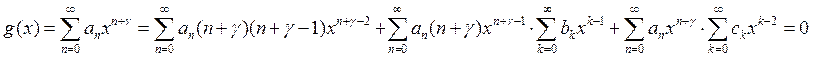 (*)
(*)
Сомнения насчет формулы.
Минимальная степень в (*) это ![]() , коэффициенты при
, коэффициенты при ![]() имеют
вид:
имеют
вид:
![]()
Получим квадратное уравнение, позволяющее определить корни ν1 и ν2:
![]()
Определим рекуррентные соотношения для коэффициентов аn:
![]()
![]()
…
![]()
Из определенного соотношения мы
находим ![]() и
и ![]() :
:
![]()
![]()
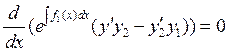 На счет этой
формулы тоже сомнения.
На счет этой
формулы тоже сомнения.
![]()
Для ряда,
соответствующего ![]() количество коэффициентов
обрывается на n. Т.е. можно записать
количество коэффициентов
обрывается на n. Т.е. можно записать ![]()
![]() , а для
, а для ![]() получим соотношение
получим соотношение ![]() , где
, где ![]() .
Остается линейная комбинация, связывающая коэффициенты
.
Остается линейная комбинация, связывающая коэффициенты ![]() ,
она должна быть равна нулю. Если это выполняется, то можно выбрать коэффициенты
,
она должна быть равна нулю. Если это выполняется, то можно выбрать коэффициенты
![]() и получить второе решение уравнения в виде
бесконечного ряда с точностью до двух произвольных параметров
и получить второе решение уравнения в виде
бесконечного ряда с точностью до двух произвольных параметров ![]() и
и ![]() . Если
не выполняется равенство нулю линейной комбинации, то можно получить только
конечный кусочек ряда с коэффициентами
. Если
не выполняется равенство нулю линейной комбинации, то можно получить только
конечный кусочек ряда с коэффициентами ![]() для
второго решения, т.е. данный метод не позволяет получить два частных решения
диф. уравнения.
для
второго решения, т.е. данный метод не позволяет получить два частных решения
диф. уравнения.![]()
![]()
![]() –
произвольное действительное число. Иногда
–
произвольное действительное число. Иногда ![]() –
комплексное число, но действительная часть должна быть не отрицательна.
–
комплексное число, но действительная часть должна быть не отрицательна.
Для уравнения Бесселя выполняются условия теоремы Фукса, значит решение можно искать в виде обобщенно степенного ряда. Если действовать аналогично гипергеометрическому ряду, то определяющее соотношение имеет вид:
![]()
Рекуррентное соотношение имеет для коэффициентов вид:
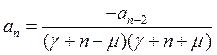
Если рассмотреть минимальную нечетную степень х, то получим соотношение:
![]()
Если разрешить это уравнение, то все нечетные коэффициенты ряда будут нулевыми и остаются только четные коэффициенты ряда, которые вычисляются по второму соотношению:
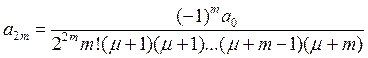
Воспользуемся свойством Г функции
и перепишем , учитывая ![]() :
:
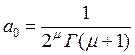
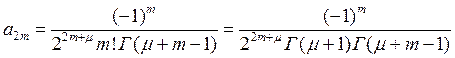
Соотношение определяет коэффициенты обобщенно степенного ряда, которое будет решением уравнения Бесселя
при ![]() . Если
. Если ![]() , то
можно определить
, то
можно определить ![]() формулой:
формулой:
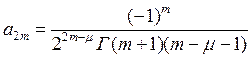
Степенной ряд с коэффициентами и для ![]() называется функцией Бесселя первого рода
порядка
называется функцией Бесселя первого рода
порядка ![]() и имеет вид:
и имеет вид:
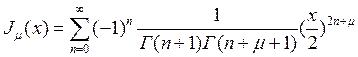
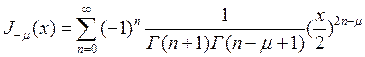
Соотношение определяет функцию Бесселя только для дробных значений ![]() ,
поскольку при целых отрицательных μ коэффициенты этого ряда не существуют. Т.к.
сама функция Бесселя непрерывна, то можно построить ее продолжение при
,
поскольку при целых отрицательных μ коэффициенты этого ряда не существуют. Т.к.
сама функция Бесселя непрерывна, то можно построить ее продолжение при ![]() , где
, где ![]() целое,
только это решение будет линейно зависимым с решением . В этом случае получается одно линейно независимое решение. Для определения второго линейно
независимого решения используют функцию Бесселя второго рода.
целое,
только это решение будет линейно зависимым с решением . В этом случае получается одно линейно независимое решение. Для определения второго линейно
независимого решения используют функцию Бесселя второго рода.
Пусть дано диф. уравнение n-го порядка:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.