Дифференциальные уравнения первого порядка, страница 9

                                         и пусть нужно найти периодическое решение этого уравнения. Тогда эти решения нужно искать в виде ряда Фурье:

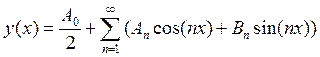
Если решение имеет период Т, то правая часть есть периодическая функция с периодом , т.е. если мы подставим  в и заменим  на , то:

и значит F должна быть периодической функцией с периодом Т. Если правая часть есть периодическая функция с периодом Т, то решение можно искать в виде ряда Фурье по функциям соответствующих периодов. Если правая часть не является периодической функцией аргумента х, то периодическое решение уравнения не существует. Если правая часть F явно не зависит от аргумента х, то ее можно рассматривать как периодическую функцию аргумента х любого периода и соответственно у уравнения существует решение любого периода.

Теория устойчивости.

Пусть дана система ДУ

                                  

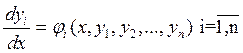
О. Решение   системы называется устойчивым по Ляпунову, если

 

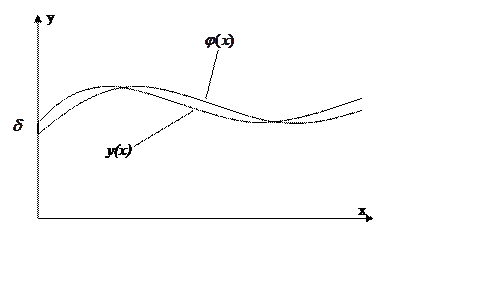
Решения близкие по начальным условиям должны быть близкими для всех х.

О. Если при малой  хотя бы для одного из решений системы неравенство не выполняется, то в этом случае решение  называется неустойчивым.

О. Если решения  не только устойчивы, но и  при условии  , то решение  называется асимптотически устойчивым.

Замечание. Из асимптотической устойчивости не следует устойчивость.

Общие Т об устойчивости систем ДУ.

Пусть дана неоднородная СЛДУ

                                          

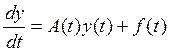
Соответствующая однородная система может быть записана в виде:

                                             

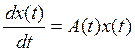
О. Линейная система называется устойчивой (вполне устойчивой), если все ее решения у(t) соответственно устойчивы по Ляпунову при .

О. Система неустойчива (вполне неустойчива), если все ее решения  неустойчивы по Ляпунову при .

Замечание. Решения ЛСДУ либо все одновременно устойчивы, либо все одновременно неустойчивы.

Т. Для устойчивости системы с любой правой частью  необходимо и достаточно, чтобы было устойчиво тривиальное решение  однородной системы .

Док-во:

Необходимость: Пусть  - некоторое решение системы .  

 – будет решение однородной системы.

 

 

тривиальное решение  будет устойчивым при  .

Замечание. Из док-ва Т следует, что устойчивость тривиального решения ОСЛДУ вытекает из устойчивости хотя бы одного решения НСЛДУ при любой правой части, в частности при .

Достаточность: Пусть тривиальное решение  устойчиво по Ляпунову при . Тогда если  – некоторое произвольное решение ОСЛДУ , то это означает, что для x(t):  . Если   - это некоторое решение НСЛДУ , а  – это произвольное решение этой же системы, то из определения  следует устойчивость по Ляпунову решения .

Следствие. СЛДУ устойчива, когда устойчиво хотя бы одно решение этой системы и вполне неустойчива, когда неустойчиво некоторое его решение.

О. СЛДУ называется равномерно устойчивой, если все решения равномерно устойчивы при  относительно начального момента .

Устойчивость называется равномерной в некоторой области, если число  можно выбирать независимо от .

Замечание. Поведение решений НСЛДУ для любой правой части  определяется решением соответствующей ОСЛДУ.

Т. СЛДУ равномерно устойчива тогда и только тогда, когда тривиальное решение ОСЛДУ равномерно устойчиво при .

О. СЛДУ называется асимптотически устойчивой, если все решения этой системы асимптотически устойчивы при .

Т. СЛДУ   асимптотически устойчива тогда и только тогда, когда тривиальное решение однородной системы асимптотически устойчиво при .

Следствие. Для асимптотической устойчивости НСЛДУ при любой правой части необходимо и достаточно, чтобы была асимптотически устойчива соответствующая ОСЛДУ.

 

Устойчивость линейных однородных систем ДУ.

Пусть дана система , где  – правые части,  – линейные непрерывные функции.

Покажем, что устойчивость системы эквивалентна ограниченности ее решений. Для этого воспользуемся следующими Т.