Дифференциальные уравнения первого порядка, страница 2

В общем случае уравнение Риккати  в квадратурах не интегрируется но его можно преобразовать в уравнение Бернулли, если известно хотя бы одно частное решение. Частное решение ищется в виде правой части

Пусть  частное решение, тогда . Получим уравнение Бернулли относительно переменной .

6) Уравнение полных дифференциалов

                                     

Причем функции и  удовлетворяют соотношению 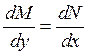 т.е. уравнение – полный дифференциал некоторой функции.

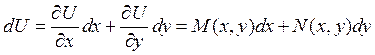
Пусть  - решение . Значит:    

Если заданны начальные условия то можно определить С. Проинтегрируем  по , будем считать  константой.

                   

  =>  

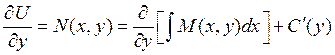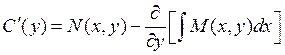
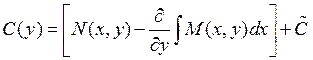
Подставим С(y) в получим

7) Уравнение Лагранжа

                                         

Продифференцируем по : .  Сделаем замену .

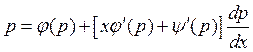
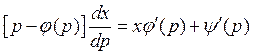
Линейное уравнение первого порядка относительно функции p. Предположим что интеграл существует. Заменив в уравнении Лагранжа на p и учитывая что  мы получили интегральные кривые в параметрической форме:

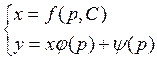
8) Уравнение Клеро

. Сделаем замену

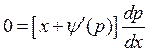
1. ; 

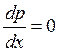Таким образом общее решение этого уравнения есть семейство прямых: .

2.

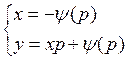
Получаем общее решение уравнения Клеро в виде параметрически заданных кривых – огибающих для кривых из пункта 1.

Теорема о существовании и единственности.

Пуст дано дифференциальное уравнение

                                                                                                                

Будем предполагать что  определенна на некотором открытом множестве Г которое принадлежит плоскости . Предположим что и ее частные производные непрерывны на множестве Г тогда:

1)  найдется решение  -  решение уравнения которое удовлетворяет условию

                                            

2) Если у уравнения существует  два решения  которые совпадают хотя бы в одной точке , т.е. . То решения  будут тождественно равны для всех значений переменной , для которых они определены.

Числа  называются начальными значениями для решения . Условие называется начальным условием.

Геометрическая интерпретация.

Через некоторую точку Г проходит только одна интегральная кривая. Решение уравнения обычно называют некоторую функцию  определенную на некотором интервале  наряду с этой функцией может быть определена некоторая  функция  определенная , которая тоже является решением .

Второй пункт теоремы утверждает, что эти решения тождественно равны на интервале на котором эти решения определены. Если интервал  содержит интервал , то решение  есть продолжение решения .

Поэтому если подразумевать под интегральной кривой график не продолжаемого решения решения, то утверждение о том что через каждую точку  проходит интегральная кривая становится точным.

Уравнения не разрешимые относительно производных.

В общем виде уравнения не разрешимые относительно производных можно записать

                                               

1) Если уравнение имеет вид:

                                                   причем существует хотя бы один действительный корень  получаем 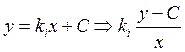  т.к.  - корень уравнения .

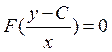
2)

                                                 

Если уравнение не разрешимо относительно , введем параметр t, и заменим двумя параметрическими уравнениями. , .

      Решение уравнения определяется кривой в параметрической форме.

Если можно разрешить относительно  т.е. , тогда в качестве параметра

3)

                                                 

Если неразрешимо относительно  то вводят параметр и заменяют на два параметрических. .

      

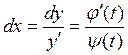
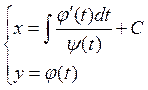
Если можно разрешить относительно , то .

4) Общий случай.

Если уравнение имеет вид то его можно попытаться разрешить если ввести параметризацию следующим образом: .

                       

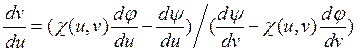
Уравнение – уравнение первого порядка  уже разрешенное относительно производной.

Уже рассмотренное уравнение Лагранжа – Клеро сводится к уравнению этого типа.