Дифференциальные уравнения первого порядка, страница 5

                                                

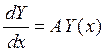
удовлетворяет  при любом t.

Матрица   и  будут решением системы . При  эти матрицы совпадают

                                              

Т.к. эти решения совпадают хотя бы в одной точке, то в силу теоремы о существовании и единственности эти решения будут совпадать во всех точках, на которой они определены.

В формуле сделаем замену .

 умножим справа на .

                                              

                           

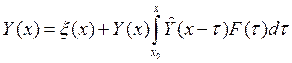
Т.е. в этом случае решение неоднородного уравнения примет вид .

ДУ (n)-го порядка

                                       

- ур-е разреш-е отн-но произв. старш. порядка.

                                    

- ур-е не разрешенное.

Уравнение (n)-го порядка можно записать в виде системы из (n) уравнений 1-го порядка:

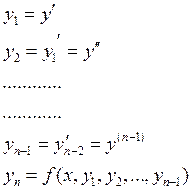                                        записи (1)~(2)~(3) эквивалентны.

Из следует, что все уравнения и теоремы для уравнений 1-го порядка верны и переносятся для уравнений (n)-го порядка, т.е. выполнены условия теоремы существования и единственности.

Простейшие случаи понижения порядка

1)  Уравнение не содержит неизвестной функции y и ее производных вплоть до порядка (k-1)

                                     

В этом случае порядок уравнения можно понизить до (n-k) порядка, если сделать замену , тогда будет иметь вид

И если это уравнение можно решить , т.е. , тогда функцию y можно получить k-кратным интегрированием функции p.

Пример:

 

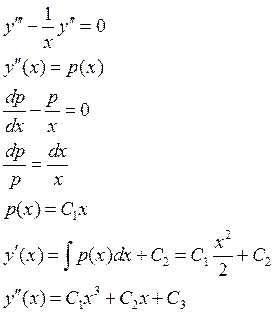
2)  Уравнение не содержит переменной x

Порядок уравнения можно понизить на единицу

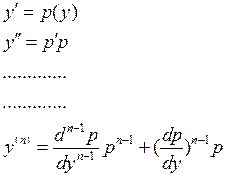
Пример:

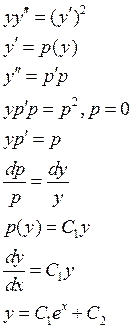
3)  Левая часть уравнения есть производная ДУ порядка (n-1)

                    

                                                    

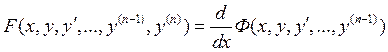
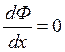
Тогда если  решение , значит мы получили первый интеграл ур-ния (5)

ЗАМЕЧАНИЕ: Для уравнений достаточно обычна ситуация когда левая часть этого уравнения становится производной функции Ф только при умножении на некоторую функцию (интегр. множитель) . Это приводит к появлению лишних решений или потери решений если  разрывная функция.

Пример:

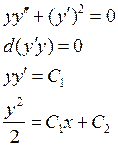
4)  Уравнение однородно относительно функции y и ее производных, т.е.

                        

Порядок можно понизить на единицу заменой

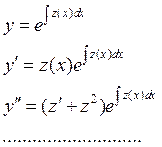
Подставим все в уравнение и мы получим уравнение на порядок ниже.

Пример:

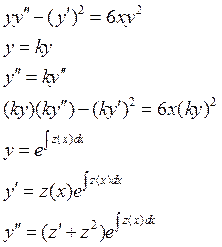         справа и слева k² – уравнение однородно.

Линейные ДУ (n)-го порядка

Определение: Линейным ДУ (n)-го порядка называется уравнение вида

                                       

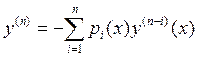
Если коэффициенты  непрерывны на , то в окрестности любых начальных значений вида: 

                 выполняются условия теоремы существования и единственности. Линейность и однородность сохраняются при любом преобразовании , где  n раз дифференцируемая функция, причем . Линейность и однородность уравнения также сохраняется при линейном и однородном преобразование к неизвестной функции y:.

Введем линейный дифференцируемый оператор

Тогда уравнение можно переписать в виде

                                                   

Определитель Вронского W(x) для будет иметь вид:

                               

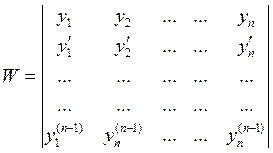
 независимые частные решения уравнения

ТЕОРЕМА1:

Если линейно-независимые функции  это решение линейного дифференциального уравнения (однородного уравнения ) с непрерывными на  коэффициентами , тогда определитель Вронского  для функций .

ТЕОРЕМА2:

Общее решение линейного однородного уравнения с непрерывными на  коэффициентами  будет линейная комбинация решений

                                            

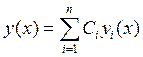
СЛЕДСТВИЕ:

Максимальное число линейно независимых решений равно его порядку.

Если нам известно не тривиальное решение , то мы можем сделать подстановку  и понизить порядок уравнения сохраняя его линейность и однородность. Обычно эту подстановку разбивают на две:

Решению  ,будет соответствовать функция , тогда подставив  в мы получим, что коэффициент , а значит сделав замену  мы получим уравнение (n-1) порядка.