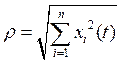 . Если исследуем знак
производной ? , то знак будет определяться следующим образом: знак
. Если исследуем знак
производной ? , то знак будет определяться следующим образом: знак ![]() совпадает со знаком
совпадает со знаком ![]() .
.
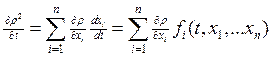
- в нем ![]() - известная функция,
значит известен ее знак. Значит можно определить знак производной
- известная функция,
значит известен ее знак. Значит можно определить знак производной ![]() (*).
(*).
Если (*) ![]() , то сама функция
, то сама функция ![]() убывающая для всех
убывающая для всех ![]() .
Все точки всех траекторий не будут удаляться от (0,0) с ростом t. Значит тривиальное решение – устойчивая т.п.
.
Все точки всех траекторий не будут удаляться от (0,0) с ростом t. Значит тривиальное решение – устойчивая т.п.
Но т.п. может быть устойчивой и даже асимптотически
устойчивой и при немонотонном приближении к ней т. траекторий с ростом t. Поэтому вместо функции ![]() или
или ![]() Ляпунов предложил рассматривать функцию
Ляпунов предложил рассматривать функцию ![]() или
или ![]() ,
которая в некотором смысле является обобщенным расстоянием от т. траектории до
начала координат. Основные свойства функции V и
,
которая в некотором смысле является обобщенным расстоянием от т. траектории до
начала координат. Основные свойства функции V и ![]() совпадают: если V
мало, то и
совпадают: если V
мало, то и ![]() мало. V – функция
Ляпунова.
мало. V – функция
Ляпунова.
Пусть дана НСДУ
![]()
![]()
- начальные условия. Пусть ![]() -
решение системы – невозмущенное движение, устойчивость которого нужно исследовать в некоторой Н-окрестности этого решения (
-
решение системы – невозмущенное движение, устойчивость которого нужно исследовать в некоторой Н-окрестности этого решения (![]() т.е.
т.е. ![]() ).
).
Положим,
![]()
![]() – отклонение решения
– отклонение решения ![]() от решения
от решения ![]() .
.
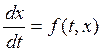
И ![]() удовлетворяет системе . Здесь
удовлетворяет системе . Здесь ![]() и значит при
и значит при ![]() ,
, ![]() . Значит система имеет тривиальное решение
. Значит система имеет тривиальное решение ![]() , которое соответствует решению
, которое соответствует решению ![]() . Систему называют возмущенной системой по Ляпунову. Исследование на устойчивость системы эквивалентно исследованию на устойчивость системы тривиального решения.
. Систему называют возмущенной системой по Ляпунову. Исследование на устойчивость системы эквивалентно исследованию на устойчивость системы тривиального решения.
О. Действительная непрерывная скалярная функция ![]() называется знакопостоянной в области D, если
называется знакопостоянной в области D, если ![]() при
при ![]() .
.
О. Функция ![]() называется положительно
определенной в области D, если существует такая
скалярная функция
называется положительно
определенной в области D, если существует такая
скалярная функция ![]() , что
, что
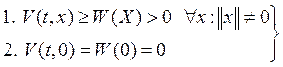
О. функция ![]() называется отрицательно
определенной в области D, если существует скалярная
функция
называется отрицательно
определенной в области D, если существует скалярная
функция ![]() :
:
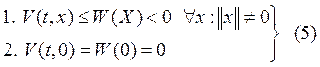 ????
????
Замечание. В качестве функции ![]() выбирают
выбирают
![]() .
.
Пусть ![]() положительно
определенная функция, удовлетворяющая условию(5) и существует соответствующая
положительно
определенная функция, удовлетворяющая условию(5) и существует соответствующая ![]() И пусть поверхности уровня ф-ии
И пусть поверхности уровня ф-ии ![]() в пространстве
в пространстве ![]() представляют
собой семейство непрерывных замкнутых поверхностей, включающих начало координат
и расширяющихся. Тогда каждая поверхность уровня функции
представляют
собой семейство непрерывных замкнутых поверхностей, включающих начало координат
и расширяющихся. Тогда каждая поверхность уровня функции ![]() будет содержаться для любых
будет содержаться для любых ![]() внутри поверхности уровня
внутри поверхности уровня ![]() .
.
Первая Т Ляпунова об устойчивости.
Пусть функция ![]() (правая часть системы ) непрерывна по t и дифференцируема по х. Рассмотрим область
(правая часть системы ) непрерывна по t и дифференцируема по х. Рассмотрим область ![]() . Система допускает тривиальное решение
. Система допускает тривиальное решение ![]() . Положим V=V(t,x) некоторую
функция непрерывно дифференцируемую по t и по х, и определенную на области
. Положим V=V(t,x) некоторую
функция непрерывно дифференцируемую по t и по х, и определенную на области ![]() .
тогда
.
тогда
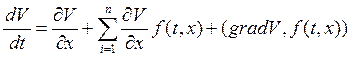 называется полной производной
называется полной производной ![]() по
по ![]() в силу системы или субстанциальной производной.
в силу системы или субстанциальной производной.
Если для возмущенной системы существует положительно определенная скалярная функция ![]() , удовлетворяющая
условиям , для которых
, удовлетворяющая
условиям , для которых 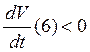 , тогда тривиальное решение
, тогда тривиальное решение ![]() системы устойчиво по Ляпунову при
системы устойчиво по Ляпунову при![]() .
.
Док-во: По условию Т существует ![]() и для V
выполняются . В пространстве
и для V
выполняются . В пространстве ![]() рассмотрим сферу радиусом
рассмотрим сферу радиусом ![]()
![]()
![]() . Эта сфера – компакт
(ограниченное замкнутое множество) и значит на компакте
. Эта сфера – компакт
(ограниченное замкнутое множество) и значит на компакте ![]() непрерывна
и положительна и по Т Вейерштрасса она будет достигать inf
и sup. Обозначим
непрерывна
и положительна и по Т Вейерштрасса она будет достигать inf
и sup. Обозначим ![]()
![]() и значит
и значит
![]()
Пусть ![]() - это некоторое
значение аргумента t из
- это некоторое
значение аргумента t из ![]() .
функция
.
функция ![]() непрерывна по х. причем
непрерывна по х. причем ![]() , значит существует окрестность
, значит существует окрестность ![]() , где
, где ![]() :
функция
:
функция ![]() и
и ![]() (*).рассмотрим
любое нетривиальное решение х(t) с начальными условиями
(*).рассмотрим
любое нетривиальное решение х(t) с начальными условиями
![]() . докажем, что траектория целиком находится
внутри сферы
. докажем, что траектория целиком находится
внутри сферы ![]() , т.е.
, т.е.
![]() при t меняющимся от 0 до
при t меняющимся от 0 до ![]() .
.
При ![]() по условию
по условию ![]() . И пусть неравенство выполняется не для всех t
. И пусть неравенство выполняется не для всех t ![]() . пусть
некоторая т.
. пусть
некоторая т. ![]() - первая т. для которой неравенство не выполняется, т.е.
- первая т. для которой неравенство не выполняется, т.е. ![]() и
и ![]() .
рассмотрим функцию V(t)=V(t,x(t)). Исследуя поведение этой функции вдоль решения х(t), т.е.
.
рассмотрим функцию V(t)=V(t,x(t)). Исследуя поведение этой функции вдоль решения х(t), т.е. 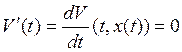 . функция V(t) невозрастающая, значит учитывая
формулу (*) и , мы получили
. функция V(t) невозрастающая, значит учитывая
формулу (*) и , мы получили ![]() по построению. Эта цепочка невозможна.
Значит решение x(t) на
интервале
по построению. Эта цепочка невозможна.
Значит решение x(t) на
интервале ![]() остается внутри сферы
остается внутри сферы ![]() и т.к. по условию
и т.к. по условию ![]() ,
то это решение х(t) бесконечно продолжаемо вправо,
причем выполняется соотношение , если
,
то это решение х(t) бесконечно продолжаемо вправо,
причем выполняется соотношение , если ![]() . а это и означает устойчивость по Ляпунову
тривиального решения
. а это и означает устойчивость по Ляпунову
тривиального решения ![]() при
при ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.