Следствие 1. При выполнении первой Т Ляпунова все
решения x(t) системы (1) с
достаточно малыми по норме начальными значениями ![]() , где
, где ![]() бесконечно продолжаемы вправо и ограничены
на полуоси
бесконечно продолжаемы вправо и ограничены
на полуоси ![]() .
.
Следствие 2. Если для ЛОСДУ ![]() ,
где
,
где ![]() , существует положительно определенная
функция V(t,x),
для которой полная производная
, существует положительно определенная
функция V(t,x),
для которой полная производная ![]() , тогда все решения x(t) этой системы определены и
ограничены на полуоси
, тогда все решения x(t) этой системы определены и
ограничены на полуоси ![]() .
.
Вторая Т Ляпунова об асимптотической устойчивости.
Пусть для системы (4) ![]() существует
положительно определенная функция
существует
положительно определенная функция ![]() , которая допускает
бесконечно малый предел при
, которая допускает
бесконечно малый предел при ![]() и полная производная
которой в силу системы (4) отрицательна
и полная производная
которой в силу системы (4) отрицательна ![]() . тогда
тривиальное решение * будет асимптотически устойчивым по Ляпунову при
. тогда
тривиальное решение * будет асимптотически устойчивым по Ляпунову при ![]() .
.
Следствие 1. условие Т2 Ляпунова ![]() тривиального решения принадлежит области
притяжения тривиального решения
тривиального решения принадлежит области
притяжения тривиального решения ![]() .
.
Следствие 2. Если для ЛОС ![]() существует
положительно определенная функция V(t,x), которая удовлетворяет условию Т2 Ляпунова, то каждое
решение этой системы асимптотически устойчиво в целом.
существует
положительно определенная функция V(t,x), которая удовлетворяет условию Т2 Ляпунова, то каждое
решение этой системы асимптотически устойчиво в целом.
Третья Т Ляпунова о неустойчивости.
Пусть для системы существует такая функция V(t,x)
непрерывно дифференцируемая по t и
по х, допускающая бесконечно малый верхний предел при ![]() и
обладающая знакопостоянной субстанциальной производной. Если при некотором
и
обладающая знакопостоянной субстанциальной производной. Если при некотором ![]() (a - начальная т.
области D) в любой
(a - начальная т.
области D) в любой ![]() -окрестности
-окрестности
![]() . ? найдется
т.
. ? найдется
т. ![]() , для которой знак функции V совпадает со знаком полной производной
, для которой знак функции V совпадает со знаком полной производной ![]() , то тривиальное решение
, то тривиальное решение ![]() будет неустойчивым по Ляпунову при
будет неустойчивым по Ляпунову при ![]() .
.
Замечание 1. В Т3 функция ![]() не
обязательно является знакопеременной.
не
обязательно является знакопеременной.
Замечание 2. Функции ![]() ,
удовлетворяющие Т1, Т2, Т3, называются соответственно функциями Ляпунова
первого, второго, третьего рода.
,
удовлетворяющие Т1, Т2, Т3, называются соответственно функциями Ляпунова
первого, второго, третьего рода.
Следствие. Если для системы (приведенная) существует функция Ляпунова 1, 2, 3-его рода, то тривиальное решение
устойчиво, асимптотически устойчиво, или неустойчиво по Ляпунову при ![]() .
.
Замечание. При формулировке Т3 предполагается, что
полная производная в силу системы ![]() знакоположительна в некоторой окрестности
начала координат. Но для док-ва неустойчивости тривиального решения системы достаточно обнаружить существование хотя бы одно траектории, исходящей из любой сколь
угодно малой окрестности начала координат и выходящей за пределы фиксированной
окрестности. Т.е нет необходимости рассматривать полную окрестность (0,0) и
условие Т Ляпунова можно ослабить.
знакоположительна в некоторой окрестности
начала координат. Но для док-ва неустойчивости тривиального решения системы достаточно обнаружить существование хотя бы одно траектории, исходящей из любой сколь
угодно малой окрестности начала координат и выходящей за пределы фиксированной
окрестности. Т.е нет необходимости рассматривать полную окрестность (0,0) и
условие Т Ляпунова можно ослабить.
Т Четаева.
Пусть дана система в области D ![]() . В
ней существует непрерывно дифференцируемая функция V(t,x), область положительности которой
. В
ней существует непрерывно дифференцируемая функция V(t,x), область положительности которой
![]() имеет ненулевое открытое сечение
имеет ненулевое открытое сечение ![]() , примыкающее к началу координат
, примыкающее к началу координат ![]() . Причем на части границы области П,
лежащей внутри цилиндра D, включающая ось t, выполняется равенство
. Причем на части границы области П,
лежащей внутри цилиндра D, включающая ось t, выполняется равенство ![]() , тогда
если
, тогда
если
1. функция ![]() ограничена в области П
ограничена в области П
2. имеет в этой области положительную полную производную ![]()
3. в каждой подобласти ![]() справедливо
неравенство
справедливо
неравенство ![]() , где
, где ![]() -
некоторая величина, зависящая от
-
некоторая величина, зависящая от ![]() , то тогда тривиальное решение системы неустойчиво по Ляпунову при * .
, то тогда тривиальное решение системы неустойчиво по Ляпунову при * .
Исследование на устойчивость по первому приближению.
Пусть есть
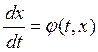 нормальная система ДУ. И пусть правая часть
нормальная система ДУ. И пусть правая часть ![]() удовлетворяет условиям Т о существовании и
единственности, может быть представлена в виде
удовлетворяет условиям Т о существовании и
единственности, может быть представлена в виде
![]()
A(t) –
матрица, F(t,x)
удовлетворяет условиям ![]() . ЛОСДУ
. ЛОСДУ ![]() называется первым приближением или
линеаризацией соответствующей нормальной системы ДУ. Согласно предположению F(t,0)=0
называется первым приближением или
линеаризацией соответствующей нормальной системы ДУ. Согласно предположению F(t,0)=0
![]()
![]() - соответствующие вектора
- соответствующие вектора ![]()
![]() - компоненты вектора х.
- компоненты вектора х.
Если A(t)=const (A(t)=A), то тогда исследование на устойчивость можно проводить,
пользуясь Т об устойчивости системы ДУ с постоянной матрицей (![]() ).
).
Задача на собственные значения или задача Штурма-Лиувилля.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.