Система линейных ДУ, сопряженная к будет иметь вид
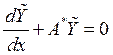
Нормальная фундаментальная система решений для : ![]() .
.
![]()
Это означает, что
![]()
Нормальные фундаментальные системы решений прямой и сопряженной задачи взаимно ортогональны.
Будем искать решение линейной системы ДУ в виде
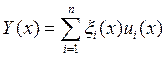
![]() – неизвестные функции,
– неизвестные функции, ![]() - нормальная
фундаментальная система решений . Подставим в , получим
- нормальная
фундаментальная система решений . Подставим в , получим 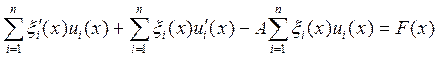 . Поскольку
. Поскольку ![]() - решение фундаментальной
системы Þ
- решение фундаментальной
системы Þ ![]() .
.
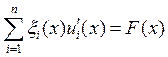
Помножим (6) скалярно на функцию ![]()
![]()
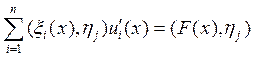 ,
, ![]()
![]() ,
, ![]()
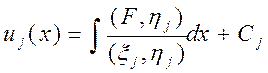 ,
, ![]()
Подставив ![]() в , получим
в , получим
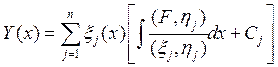
Замечание: метод Коши применяется только в том случае, когда можно построить две взаимно ортогональные нормальные системы фундаментальных решений.
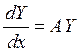
A – матрица с постоянными коэффициентами.
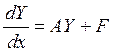
Решение системы будем искать в виде ![]() ,a - вектор,l-скаляр.
,a - вектор,l-скаляр.
Подставим решение в систему .
![]() ,
, ![]()
![]()
![]() ,
, ![]() -собственные значения
матрицы A,
-собственные значения
матрицы A, ![]() -собственные
векторы матрицы A.
-собственные
векторы матрицы A.
Вид решения будет зависеть от l.
1) Все собственные значения A действительны и различны. Это означает, что любое частное решение системы будет иметь вид:
![]() ,
, ![]()
И следовательно общее решение однородной системы (1) будет иметь вид:
![]()
Воспользуемся теоремой линейной алгеброй о представлении матрицы A в следующем виде, при условии, что все ее собственные значения действительны и различны.
![]() ,
, ![]()
Подставим это представление в систему :
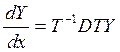 ,
,
![]()
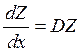
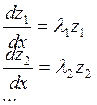 мы
получили n уравнений с разделяющими
переменными.
мы
получили n уравнений с разделяющими
переменными.
Решением этих уравнений
будет ![]()
![]()
![]()
2) Одно из собственных значений A комплексное. Поскольку матрица A изначально была вещественна – это
означает, что ![]() сопряженное
сопряженное ![]() и
и ![]() . Общее
решение будет иметь вид аналогичный . Поскольку исходный оператор был
вещественнозначный, то и общее решение системы может быть представлено в виде
линейной комбинации частных вещественных реешний.
. Общее
решение будет иметь вид аналогичный . Поскольку исходный оператор был
вещественнозначный, то и общее решение системы может быть представлено в виде
линейной комбинации частных вещественных реешний.
Теорема:
Если
оператор 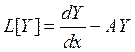 вещественный, а
вещественный, а ![]() и
и
![]() функции принимающие вещественные значения,
такие что
функции принимающие вещественные значения,
такие что ![]() есть решение
есть решение ![]() , тогда
, тогда
![]() и
и ![]() тоже
будут решениями этого однородного уравнения.
тоже
будут решениями этого однородного уравнения.
3) Собственное значение имеют кратность g. В этом случае для матрицы A строится ЖНФ и общее решение (1) имеет вид:
![]() , l - собственное значение.
, l - собственное значение.
Вид решения выводится так же, как для системы когда матрица A имеет все действительные корни.
Пусть дано матричное дифференциальное уравнение
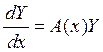
где
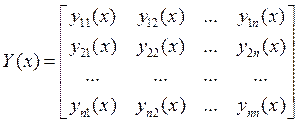
![]()
- начальное условие
Теорема:
Если матрица
![]() непрерывна на отрезке
непрерывна на отрезке ![]() , а
, а ![]() , то на
отрезке
, то на
отрезке ![]()
![]() единственное решение
уравнения определитель Вронского этой
матрицы не равен 0 для любой точки
единственное решение
уравнения определитель Вронского этой
матрицы не равен 0 для любой точки ![]() .
.
Одновременно с системой будем рассматривать сопряженную систему
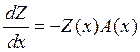
Теорема:
Пусть ![]() - решение системы , матрица
- решение системы , матрица ![]() непрерывна
на
непрерывна
на ![]() , тогда
, тогда ![]()
![]() на
на ![]() и
является решением системы .
и
является решением системы .
Рассмотрим систему неоднородных дифференциальных уравнений
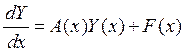
Будем искать решение в виде вариации постоянных
![]()
![]() - решение системы ,
- решение системы , ![]() -
решение системы ,
-
решение системы , ![]() – неизвестный
вектор функций.
– неизвестный
вектор функций.
Подставим в
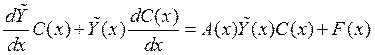
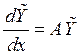
![]()
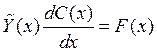
![]()
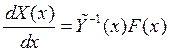
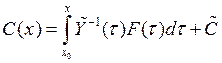
тогда общее решение примет вид
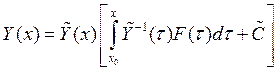
Общее решение неоднородной системы может быть представлено в виде:
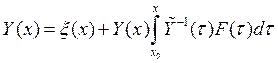
![]() -
общее решение системы
-
общее решение системы
Замечание:
Пусть
матрица A – постоянна, а начальное условие
имеет вид ![]() . Покажем, что решение системы
. Покажем, что решение системы
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.