Дифференциальные уравнения первого порядка, страница 7

                                 

Если на  коэффициенты  и правая часть  непрерывные функции, то уравнение удовлетворяет начальным условиям

                                        и имеет на этом отрезке единственное решение.

Если в явно выразить старшие производные, то мы получаем уравнение такое, что правая часть уравнения удовлетворяет условиям теоремы «О существовании и единственности».

Поскольку оператор L линейный, то для него выполняется:

1.  ,будет решением , если  решение соответствующего однородного уравнения, а  частное решение неоднородного уравнения.
2.  , y_i – решения вот таких уравнений, то тогда

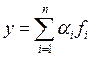
Это свойство справедливо и для , если ряд 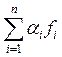 сходится и допускает n – кратное (n – порядок ДУ) по членное дифференцирование.

3. Пусть дано операторное уравнение представленное в комплексном виде:

 – линейный оператор с вещественными коэффициентами . Функции  и  тоже вещественны, тогда если это уравнение имеет решение , то решение этого же уравнения будут соответствующие действительные и мнимые части, причем каждое из решений соответствует решению операторного уравнения , .

ТЕОРЕМА:

Общее решение неоднородного уравнения n-го на отрезке , при условии, что все коэффициенты  и  непрерывны, может быть представлено в виде суммы общего решения соответствующей однородной системы 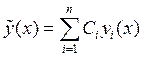    и частного решения неоднородной системы , т.е. .

Если невозможно подобрать в явном виде частное решение неоднородного уравнения, то можно воспользоваться методом вариаций постоянных. Если решение однородной системы 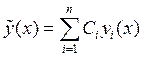, то будем искать решение в виде

                                            

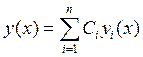
Подставим в . Нам необходимо найти n неизвестных функций, а у нас есть только одно уравнение . Тогда для оставшихся уравнений мы можем выбрать произвольные дополнительные условия:

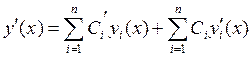
Если мы будем считать, что  ведет себя как const, тогда выберем условия следующим образом:

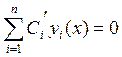
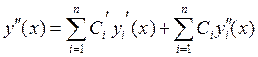
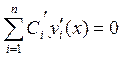
При вычислении n-ой производной мы получим

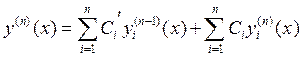, поэтому выражение для  n-ой производной можно подставить в и после приведения подобных получим вот такое условие:

                                        

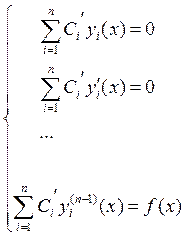
Т.о. мы получили систему из n уравнений с n неизв., причем det(5) = W(x) – определитель Вронского.

 

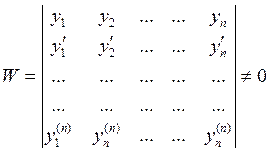
Т.е. у системы существует единственное решение

Пример:

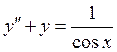
1.   

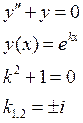
Частные решения

Частными решениями будут действительные и мнимые части

2. 

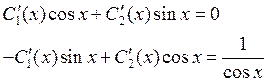
 Подставляем в общее решение и т.д.

Интегрирование дифференциальных уравнений с помощью рядов.

1.Теорема об аналитичности решения.

Пусть дано линейное диф. уравнение 2-го порядка

                                  

Если   аналитические функции аргумента  в окрестности точки , то решения уравнения тоже будут аналитическими функциями в окрестности точки  и их можно представить в виде

                                              

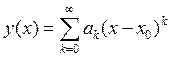
2. Теорема о разложимости решения дифференциального уравнения в обобщенно степенной ряд.

Если дифференциальное уравнение удовлетворяет условиям уравнения , но при этом функция  является нулем порядка   в точке : . Функция  имеет нуль порядка  в точке  или выше и функция имеет нуль порядка не ниже  в точке  . Тогда существует  хотя бы одно не тривиальное решение  уравнения , которое представимо в виде обобщенно степенного ряда

                                         

                                        

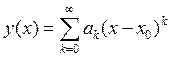
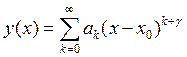
Замечание:

1.  Второе линейно независимое решение имеет вид обобщенно степенного ряда или может быть представлено в виде произведения на .

2.  В конкретных задачах подбирают степенной или обобщенно степенной ряд формально удовлетворяющий уравнению , т.е. при подстановке решения в получим соотношение для определения коэффициентов  в случае степенного ряда, и коэффициентов ,  в случае обобщенного степенного ряда. Полученный ряд исследуется на сходимость и вычисляется сумма ряда, которая будет решением диф. уравнения. Линейная комбинация полученных частных решений дает общее решение