![]()
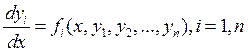
![]()
Система вида называются системой обыкновенных ДУ. Также как для ДУ, для системы ДУ можно сформулировать теорему о существовании и единственности.
Теорема: Если функции fi определены и непрерывны на открытом множестве Г, а ![]() j,i=1,n тоже непрерывны на множестве Г, тогда имеет решение
j,i=1,n тоже непрерывны на множестве Г, тогда имеет решение ![]() , i=1,n, а при наличие начальных условий,
, i=1,n, а при наличие начальных условий,
![]()
это решение будет единственным.
В векторной форме можно записать:
![]()
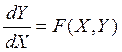
![]()
![]()
Система ДУ называется линейной, если она линейна относительно всех неизвестных функций и их производных.
![]()
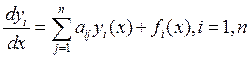
![]()
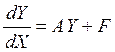
Если заданы начальные условия
![]()
то решение будет единственно.
Введем линейный оператор 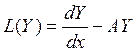 .
Тогда можно переписать в виде
.
Тогда можно переписать в виде
![]()
Если ![]() , то
, то ![]() , то система уравнений называется однородной.
, то система уравнений называется однородной.
Поскольку оператор линейный:
1. ![]() – решение однородной системы , то
– решение однородной системы , то ![]() ,
, ![]() , - решение уравнения . Т.е.
, - решение уравнения . Т.е. ![]() .
.
2. ![]() – решения , то
– решения , то ![]() тоже решение .
тоже решение .
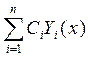 - решение при условии, что
- решение при условии, что ![]() – решение .
– решение .
Пусть ![]() – решения и они линейно
независимы. Любая
– решения и они линейно
независимы. Любая 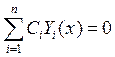 Û
Û ![]() Þ что определитель состоит из
решений
Þ что определитель состоит из
решений ![]()
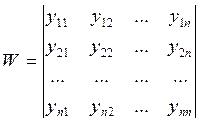 ¹0
¹0
Этот определитель называется определителем Вронского
для системы решений ![]() .
.
Теорема 1: Если определитель Вронского для с непрерывными на отрезке ![]() коэффициентами матрицы
коэффициентами матрицы![]() равен 0 хотя бы в одной точке
равен 0 хотя бы в одной точке ![]() , то решения
, то решения ![]() будут линейно зависимыми на этом отрезке, и,
следовательно, определитель Вронского равен нулю на всем отрезке
будут линейно зависимыми на этом отрезке, и,
следовательно, определитель Вронского равен нулю на всем отрезке ![]() .
.
Совокупность решений ![]() однородной системы называется фундаментальной
системой на
однородной системы называется фундаментальной
системой на ![]() , если
, если ![]() для этой системы
для этой системы ![]() .
.
Если для заданы начальные условия ![]() ,
, ![]() – единичная матрица, то система решений
– единичная матрица, то система решений ![]() называется нормальной
фундаментальной системой решений.
называется нормальной
фундаментальной системой решений.
Замечание: если ![]() – фундаментальная система решений, то линейная комбинация
– фундаментальная система решений, то линейная комбинация 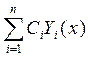 - тоже общее решение .
- тоже общее решение .
Теорема 2: 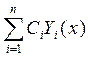 - линейная комбинация n линейно независимых решений
системы с непрерывными на отрезке
- линейная комбинация n линейно независимых решений
системы с непрерывными на отрезке ![]() коэффициентами матрицы
коэффициентами матрицы ![]() будет общим решением системы на этом отрезке.
будет общим решением системы на этом отрезке.
Теорема 3: Если ![]() - решение , а
- решение , а ![]() -
решение , то
-
решение , то ![]() +
+![]() тоже будет решением системы .
тоже будет решением системы .
Теорема 4: Общее решение неоднородной системы на ![]() с
непрерывными на отрезке
с
непрерывными на отрезке ![]() коэффициентами матрицы
коэффициентами матрицы ![]() и правыми частями
и правыми частями ![]() равно
сумме общего решения соответствующей однородной системы и частного решения неоднородной
системы .
равно
сумме общего решения соответствующей однородной системы и частного решения неоднородной
системы .
Теорема 5 (принцип суперпозиции): Решение системы ДУ вида 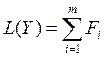 может быть представлено в виде суммы m решений
может быть представлено в виде суммы m решений 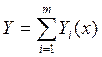 ,
каждое из которых удовлетворяет соответствующему неоднородному уравнению
,
каждое из которых удовлетворяет соответствующему неоднородному уравнению ![]() .
.
Замечание: принцип суперпозиции можно распространить и при ![]() . В этом случае решением будет ряд,
составленный из
. В этом случае решением будет ряд,
составленный из ![]() и такое представление возможно,
если ряд сходится и допускает почленное дифференцирование.
и такое представление возможно,
если ряд сходится и допускает почленное дифференцирование.
Пусть 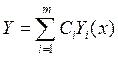 – это общее решение
однородной системы , тогда будем искать решение
неоднородной системы
– это общее решение
однородной системы , тогда будем искать решение
неоднородной системы 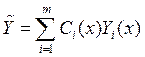 где
где ![]() – неизвестные скалярные
функции. Подставим
– неизвестные скалярные
функции. Подставим ![]() в
уравнение :
в
уравнение :
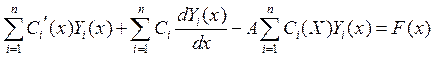
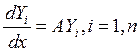
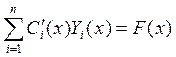
Это векторное уравнение всегда разрешимо, т.к. ![]() – это система фундаментальных решений
однородной системы . Определитель
– это система фундаментальных решений
однородной системы . Определитель ![]()
![]() . И разрешая эту
систему, получим
. И разрешая эту
систему, получим ![]() ,
, ![]() .
.
![]() ,
,![]() , где
, где ![]() - произвольные константы.
- произвольные константы.
И тогда общее решение неоднородного уравнения
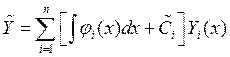
Пусть дана система линейных ДУ:
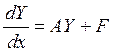
Соответствующая ей однородная система
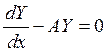
имеет нормальную фундаментальную
систему решений ![]() .
.
Определим понятие сопряженной задачи.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.