Подготовка строительства склада ГСМ под обеспечение производственной программы разреза «Кокуйский», установленной техническим заданием в объеме добычи и отгрузки каменного угля за период навигации 300 тыс. т/год, страница 14

Элементы горизонтального цилиндрического резервуара подвергаются воздействию нагрузок: гидростатическое давление жидкости; избыточное давление паров жидкости; вакуум; собственный вес; ветровая нагрузка; снеговая нагрузка.

Нагрузка в виде гидростатического давления зависит от плотности хранимой жидкости и глубины отсчета от ее поверхности, т.е.

,                                 (4.4.1)

где    = 1.1;

         р_ж - плотность жидкости;

h - глубина отсчета от поверхности жидкости.

Величина избыточного давления задается

,                                            (4.4.2)

где   

Расчетная величина вакуума принимается равной

,                                           (4.4.3)

где . [3].

4.4.2 Определение снеговой нагрузки

Определение снеговой нагрузки производят в соответствии c требованиями раздела 5 СНиП 2.01.07-85  (дополнение 2) [8].

Полное нормативное значение снеговой нагрузки на горизонтальную проекцию покрытия s определяется по формуле:

,                                            (4.4.4)

где       S_g – расчетное значение веса снегового покрова на 1 м² горизонтальной поверхности земли, принимаемое в соответствии п. 5.2 СНиП 2.01.07-85 (дополнение 2);

μ – коэффициент перехода от веса снегового покрова земли к снеговой нагрузке на покрытие, принимаемый в соответствии с пп.5.3-5.6 и схеме 2 приложения 3 СНиП 2.01.07-85.

Значение коэффициента µ можно принять равное 1,0 по всему покрытию.

Согласно СНиП 2.01.07-85^* Мотыгинский р-н относится к IV снеговому району, где  S_g=2,4 кПа.

Подставляя данные значения в формулу (3.1), получаем что снеговая нагрузка равна:

S=2,4^.1=2,4 кПа. [8]

4.4.3 Определение ветровой нагрузки

В соответствии с требованиями раздела 6 СНиП 2.01.07-85^*[8] при назначении ветровых нагрузок,  действующих на внешние и внутренние поверхности покрытия резервуаров, учитываются действия средней w_m и пульсационной составляющей ветрового давления w_p.

Нормативное значение средней составляющей ветровой нагрузки на высоте z над поверхностью земли следует определять по формуле:

,                            (4.4.5)

где  – нормативное значение ветрового давления в зависимости от ветрового района, принимаемого по (п. 6.4 СНиП 2.01.07-85^*[8]), 0,30 кПа для Мотыгинского р-на;

‑ коэффициент, учитывающий изменение ветрового давления по высоте , определяется в зависимости от типа местности, принимаем его по п. 6.5. СНиП 2.01.07-85^*[8]  k=0,50;

с – аэродинамический коэффициент, зависящий от формы сооружения. Можно принять с=0,50 по всей окружности, т.е. ветровую нагрузку заменяют условным вакуумом.

.

Нормативное значение пульсационной составляющей ветровой нагрузки на высоте z следует определять по формуле:

,                                (4.4.6)        где    ξ – коэффициент пульсации давления ветра на уровне z, принимаемый по таблице и равен 1,22;

ζ – коэффициент динамичности, ζ=1,2 ;

ν – коэффициент пространственной корреляции пульсаций давления ветра, ν =0,8.

.

Суммарное расчетное значение ветровой нагрузки определяют по формуле:

                        (4.4.7)

где    γ_t = 1,4 – коэффициент надежности по нагрузке см. п. 3.2.3 СНиП 2.01.07-85.

.

Численные исследования тонкостенных резервуаров, показали следующее: нормальные напряжения в стенке резервуара от собственного веса не превышают 0,05 кН/см², от ветровой нагрузки (для II района) не более 0,22 кПа, снеговая нагрузка нагрузка также вызывает малые значения нормальных напряжений 2,4 кПа, поэтому в дальнейшем исключены из рассмотрения нагрузки от собствено веса, ветра и снеговой нагрузки [8].

4.4.4 Расчет стенки резервуара

Стенка горизонтального цилиндрического резервуара представляет собой замкнутую цилиндрическую оболочку средней длины (0,5 <lfr< 10), свободно опирающуюся на две опоры.

Коническое днище резервуара представляют безмоментной пологой конической оболочкой под давлением.

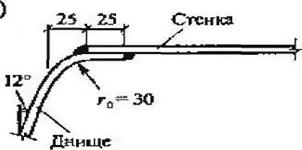
Рисунок - 2. Фрагмент типового конического днища.

Толщина стенки резервуара определяется из условия прочности (не должна быть менее 4 мм) и проверяется на устойчивость.