Тепловые процессы формирования отливок, страница 7

На пресс-формах литья под давлением, жидкой штамповки разделительный слой с целью обеспечения размерной точности и чистоты поверхности не превышает 0,1 мм. В этом случае теплоаккумулирующей способностью разделительного слоя можно пренебречь. Для преодоления расчетных затруднений, связанных с определением температуры внутренней поверхности формы и наружной поверхности отливки воспользуемся следующим упрощением задачи. При длительной выдержке отливки в металлической форме средние величины температуры отливки и формы сближаются – форма нагревается, а отливка охлаждается (рис. 49) и стремятся к некоторой одинаковой температуре Т_к – средней калориметрической температуре. Величина средней калориметрической температуры находится из алгебраического уравнения теплового баланса, в котором количество тепла, теряемое отливкой при охлаждении до средней калориметрической температуры, приравнивается количеству тепла, приобретаемому формой при нагреве от начальной до средней калориметрической температуры:

, где М₀ – масса отливки; М_ф – масса формы; С₀ – удельная теплоемкость материала отливки; С_ф – удельная теплоемкость материала формы; L – удельная теплота кристаллизации сплава; Т_зал – температура заливки металла; Т_ф.н – начальная температура формы.

После преобразования данного алгебраического уравнения получим:

.

И тогда

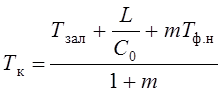, где .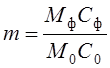

Полученное выражение средней калориметрической температуры не учитывает потери тепла с наружной поверхности формы в окружающую среду. Эти потери можно учесть следующим образом:

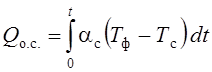, где a_с – коэффициент теплоотдачи на воздух; Т_ф – температура формы; Т_с – температура среды (воздуха).

И средняя калориметрическая температура в уточненном виде представится:

.

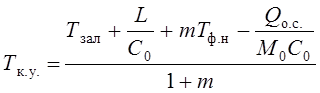Применение понятия средней калориметрической температуры позволяет рассматривать процесс затвердевания и охлаждения отливки в массивной металлической форме как процесс при постоянной температуре среды и постоянном коэффициенте теплопередачи от отливки к форме.

Весь процесс теплового взаимодействия между отливкой и формой представим в виде длительности трех последовательных стадий:

1)  снятия теплоты перегрева металла отливки;

2)  непосредственно затвердевания отливки;

3)  охлаждения затвердевшей отливки до температуры выбивки.

Для расчета длительности снятия теплоты перегрева запишем уравнение теплового баланса в дифференциальной форме:

.

В левой части уравнения элементарное количество тепла, передаваемое от отливки в среду со средней калориметрической температурой. В правой части уравнения – снижение теплосодержания отливки при охлаждении жидкого металла отливки на элементарную температуру dТ₀.

После разделения переменных и интегрирования дифференциального уравнения с пределами интегрирования: при t = 0 Т₀ = Т_зал, а при t = t_пер Т₀ = Т_лик; здесь t_пер – длительность снятия перегрева; Т_лик – температура ликвидуса сплава; получим: .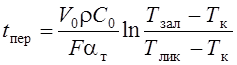

Длительность стадии собственно затвердевания отливки рассчитаем для сплава, затвердевающего в некотором интервале температур ликвидус – солидус. Применим прием, описанный ранее, введением понятия удельной эффективной теплоемкости сплава: .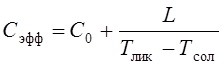

Дифференциальное уравнение теплового баланса для затвердевания запишется:

.

По аналогии с решением предыдущего дифференциального уравнения введем краевые условия: при t = 0 T₀ = Т_лик, а при t = t_затв T₀ = Т_сол и получим:

.

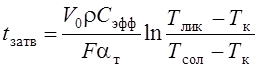Подчеркнем, что рассчитанная длительность затвердевания учитывает удельную теплоту кристаллизации в виде эффективной удельной теплоемкости.

Длительность третьей стадии – охлаждения твердой отливки с температуры солидуса до температуры выбивки рассчитываем по аналогичной методике. Составим дифференциальное уравнение теплового баланса для твердой отливки:

.

Краевые  условия  для  данного  случая:  при t = 0 T₀ = Т_сол, а при  t  =  t_выб  T₀ = Т_выб, где Т_выб – технологическая температура выбивки отливки из формы.