Тепловые процессы формирования отливок, страница 2

Для сплава, затвердевающего в некотором интервале температур от ликвидуса до солидуса, кривая охлаждения представлена на рис. 43.

На кривой охлаждения также выделены три характерных области: I – снятие теплоты перегрева со скоростью охлажде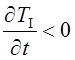ния ; II – собственно затвердевание, где скорость охлаждения 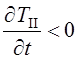; III – охлаждение твердой отливки со скоростью 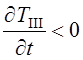. В отличие от затвердевания чистого металла для сплава 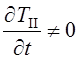, но абсолютная величина скорости затвердевания 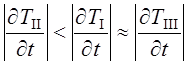 по причине выделения в зоне II скрытой теплоты затвердевания.

3.2. Расчетные методы затвердевания и охлаждения отливок

Физическая модель расчетной схемы затвердевания и охлаждения отливок может быть рассмотрена на следующей экспериментальной схеме измерения температуры отливки "плита" в различные временные отрезки на разном расстоянии от оси плиты (рис. 44). Семейство кривых, изображенных на данном рисунке, представляет температурное поле отливки "плита" для ее симметричной половины, отсчитываемой от оси плиты: Т = f (x, t). Основные тепловые параметры, определяющие затвердевание и охлаждение отливки выявляются из анализа температурного поля. Так скорость охлаждения представляет частную производную от температуры по времени: 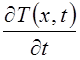. Температурный градиент – частная производная от температуры по координате "х": 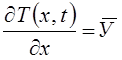 и представляет собой вектор (как производная от скалярной величины по координате). Вектор градиента температуры направлен от поверхности к оси плиты. Другой вектор – удельный тепловой поток: 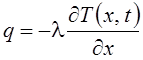 направлен в противоположном направлении – он пропорционален градиенту температуры. Коэффициент теплопроводности "l" здесь выполняет роль коэффициента пропорциональности.

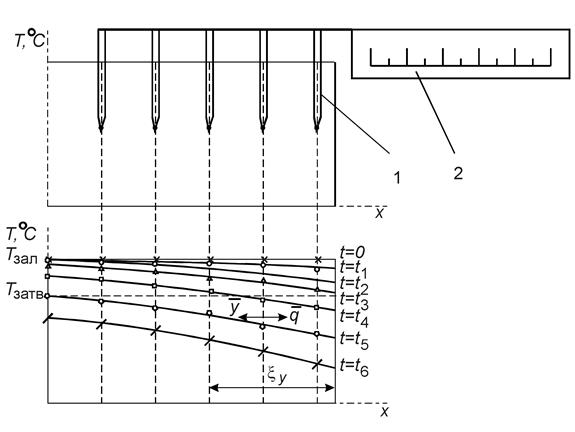
Рис. 44. Температурное поле отливки "плита":

1 – термопара; 2 – многоточечный потенциометр

По точкам пересечения горизонтальной линии, соответствующей температуре затвердевания, с кривыми соответствующими температурам Т(х) для разных периодов времени можно судить о ходе затвердевания – толщина затвердевшего слоя (x) представляет как функцию времени: . Так к моменту времени t₄ толщина затвердевшего слоя отливки составит x₄. А полное время затвердевания будет отвечать условию, когда температура в центре плиты достигнет температуры затвердевания (а точнее несколько ниже этого значения). Таким образом, в основу расчетной схемы следует положить условие расчета температурного поля отливки Т(х, t), и выявление времени достижения температуры затвердевания (температуры солидуса) в центре отливки.

3.2.1. Математическая модель расчетной схемы затвердевания

На основе сформулированной физической модели затвердевания и охлаждения отливки опишем математическую модель для отливки "плита" в виде внутренней задачи; т.е. первоначально без учета теплового взаимодействия с литейной формой.

На рис. 45 схематично представлена температура отливки по ее толщине для некоторого промежуточного времени t, когда затвердела некоторая корка твердого металла толщиной x₁. Схема представляет затвердевание чистого металла, характеризующегося температурой кристаллизации – Т_зат. На данной схеме Т₁(х, t₁) – температура жидкой части металла отливки, а Т₃(х, t₁) – температура твердой части отливки, Т₀ – температура наружной поверхности отливки.

В соответствии с физической моделью время образования затвердевшей корки толщиной x₁ и время полного затвердевания отливки, когда x достигнет значения R – половины толщины плиты, можно рассчитать на основе составления и решения дифференциальных уравнений Фурье для твердой и жидкой частей отливки.

Дифференциальное уравнение теплопроводности Фурье для твердой части отливки представляем:

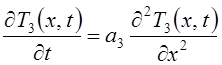 для R-x < х < R, где а₃ – коэффициент температуропроводности металла отливки.