Интеграл этот не берется, и потому для приближенного решения применяют разложение в ряд
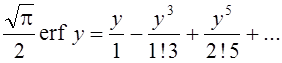 .
.
И тогда результат решения выразится в виде:
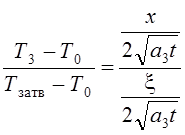 .
.
|
|
|
Рис. 48. Зависимость скорости затвердевания от времени по закону квадратного корня |
Здесь величины: Т0, Тзатв., а3
– постоянные, Т3 – температура твердой части отливки на
глубине х. Отсюда записывают: ![]() , так называемый закон
квадратного корня, устанавливающий функциональную зависимость толщины
затвердевшего слоя от времени. Здесь константа «m»
учитывает ряд перечисленных выше параметров.
, так называемый закон
квадратного корня, устанавливающий функциональную зависимость толщины
затвердевшего слоя от времени. Здесь константа «m»
учитывает ряд перечисленных выше параметров.
Анализируя закон квадратного корня, можно видеть, что с течением времени скорость затвердевания снижается
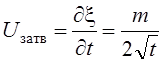 ;
;
графически толщина затвердевшего слоя как функция времени представляется параболой с показателем n = 1/2 (рис. 48). Очень простая математическая зависимость закона квадратного корня имеет ограниченное применение преимущественно для отливок из одного сплава и при небольшой разнице в толщинах стенок.
3.2.5. Приближенный расчет затвердевания отливки в тонкостенной
водоохлаждаемой металлической форме
Затвердевание и охлаждение отливки в тонкостенной водоохлаждаемой металлической форме протекает с большой интенсивностью теплообмена. Расчетная схема может быть существенно упрощена, если пренебречь аккумуляцией тепла тонкостенной формой. Ошибка расчета тем меньше, чем больше масса отливки и меньше толщина стенки формы. В этом случае принимается, что все тепло от отливки передается охлаждающей воде. Величина теплового потока, передаваемого от отливки охлаждающей воде, выразится:
![]() , где Тмет – температура металла отливки; ее
значение приближенно можно принять:
, где Тмет – температура металла отливки; ее
значение приближенно можно принять: 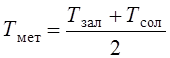 ; Тзал
– температура заливаемого металла; Тсол – температура
солидуса сплава; F – площадь поверхности
контакта отливки с формой; aт
– коэффициент теплопередачи от отливки к охлаждающей воде;
; Тзал
– температура заливаемого металла; Тсол – температура
солидуса сплава; F – площадь поверхности
контакта отливки с формой; aт
– коэффициент теплопередачи от отливки к охлаждающей воде;
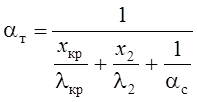 , где хкр – толщина слоя краски (смазки) на рабочей
поверхности формы; lкр – коэффициент
теплопроводности материала краски; х2 – толщина стенки
металлической формы; l2 –
коэффициент теплопроводности материала формы; aс
– коэффициент теплоотдачи к охлаждающей воде (берется по справочным данным как
функция скорости движения охлаждающей воды); Тв – температура
охлаждающей воды, берется как средняя арифметическая величина между
температурами воды на входе и выходе из формы.
, где хкр – толщина слоя краски (смазки) на рабочей
поверхности формы; lкр – коэффициент
теплопроводности материала краски; х2 – толщина стенки
металлической формы; l2 –
коэффициент теплопроводности материала формы; aс
– коэффициент теплоотдачи к охлаждающей воде (берется по справочным данным как
функция скорости движения охлаждающей воды); Тв – температура
охлаждающей воды, берется как средняя арифметическая величина между
температурами воды на входе и выходе из формы.
Количество тепла, выделяемого при затвердевании слоя толщиной dx представим:
![]() , где r – плотность сплава; Lэфф – эффективная удельная теплота кристаллизации
сплава, в которой учтен перегрев сплава:
, где r – плотность сплава; Lэфф – эффективная удельная теплота кристаллизации
сплава, в которой учтен перегрев сплава: ![]() ; L – справочная величина удельной теплоты затвердевания; с
– удельная теплоемкость сплава.
; L – справочная величина удельной теплоты затвердевания; с
– удельная теплоемкость сплава.
Составляя и решая дифференциальное уравнение теплового баланса, получим:
![]() ,
,
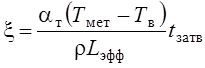 .
.
Приближенный расчет дает линейную зависимость между толщиной затвердевшей корки и временем затвердевания. Для плоской отливки время затвердевания рассчитывают, приравнивая x половине толщины стенки.
3.2.6. Приближенный расчет затвердевания отливки
в массивной металлической форме
Массивные металлические формы: кокили, пресс-формы литья под давлением, изложницы для литья слитков, изложницы для центробежного литья, формы для жидкой штамповки имеют большую толщину стенки и соответственно обладают большой теплоаккумулирующей способностью. Тепловая работа указанных металлических форм связана с толщиной разделительного слоя краски (смазки) на рабочей поверхности. На кокилях, изложницах толщина краски из огнеупорного малотеплопроводного материала значительная и составляет от десятых долей до нескольких миллиметров.
|
|
|
Рис. 49. Схема к расчету средней калориметрической температуре |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.