Дифференциальное уравнение теплопроводсности Фурье для жидкой части отливки имеет вид:
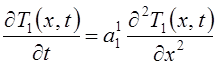 для 0 < х < R-x, где
для 0 < х < R-x, где ![]() – коэффициент
температуропроводности жидкого металла отливки.
– коэффициент
температуропроводности жидкого металла отливки.
Но поскольку в жидком металле теплопередача происходит не только теплопроводностью,
но и конвекцией, то коэффициент ![]() следует рассматривать
как некоторую эффективную температуропроводность, учитывающую теплопередачу
теплопроводностью и конвекцией.
следует рассматривать
как некоторую эффективную температуропроводность, учитывающую теплопередачу
теплопроводностью и конвекцией.
Коэффициент температуропроводности выражается
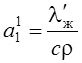 , где l – коэффициент
теплопроводности; с – удельная теплоемкость; r - плотность металла.
, где l – коэффициент
теплопроводности; с – удельная теплоемкость; r - плотность металла.
Величину коэффициента теплопроводности в жидкой фазе представим в виде фиктивной величины, одновременно учитывающей и теплопередачу конвекцией:
![]() , где l – определяющий размер отливки
(обычно высота); a – коэффициент теплоотдачи
при конвекции, определяемый из критериальных зависимостей для естественной
конвекции; lж – коэффициент
теплопроводности жидкого металла.
, где l – определяющий размер отливки
(обычно высота); a – коэффициент теплоотдачи
при конвекции, определяемый из критериальных зависимостей для естественной
конвекции; lж – коэффициент
теплопроводности жидкого металла.
Для решения двух представленных дифференциальных уравнений необходимо определится с условиями однозначности: начальными и краевыми условиями.
Начальное условие, фиксирующее состояние отливки сразу после окончания заполнения, получит вид:
![]() , где Тзал – температура заливки металла.
, где Тзал – температура заливки металла.
Краевые условия выразим для трех границ формирующейся отливки:
1. в центре отливки
"плита" в виде исследования функции на экстремум; считаем, что на оси
плиты температура максимальна во все временные периоды: 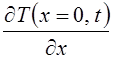 ,
т.е. частная производная от температуры по координате равна нулю;
,
т.е. частная производная от температуры по координате равна нулю;
2. на границе раздела твердая - жидкая фаза в виде равенства удельных тепловых потоков в жидкой и твердой фазах:
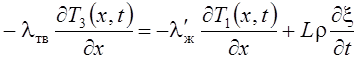 ,
,
|
|
|
Рис. 46. Температура отливки "плита" на промежуточной стадии затвердевания из сплава, кристаллизующегося в интервале температур ликвидус-солидус |
где x – толщина затвердевшей корки; L – удельная теплота затвердевания; r – плотность твердого металла;
3. на наружной поверхности отливки в виде задания функции Т0 = f(t) или в частном случае Т0 = const.
Сформулируем математическую модель затвердевания отливки "плита" из сплава, кристаллизующегося в некотором интервале температур Тлик – Тсол. Схематично температурное поле такой отливки представлено на рис. 46, где Т1(х, t) по аналогии с предыдущей схемой представляет температуру жидкой части отливки, Т3(х, t) – температуру твердой части отливки, а Т2(х, t) – температуру двухфазной твердожидкой части.
Дифференциальное уравнение Фурье для твердой зоны отливки подобно предыдущему случаю записано:
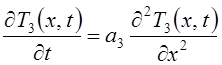 для R-x < х < R.
для R-x < х < R.
Дифференциальное уравнение теплопроводности для жидкой зоны отливки:
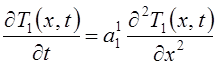 для 0 < х < R-x.
для 0 < х < R-x.
По аналогии ![]() – эффективный коэффициент
температуропроводности, учитывающий теплопередачу не только теплопроводностью,
но и конвекцией.
– эффективный коэффициент
температуропроводности, учитывающий теплопередачу не только теплопроводностью,
но и конвекцией.
Дифференциальное уравнение теплопроводности для твердожидкой зоны отливки представим как уравнение с внутренними источниками тепла:
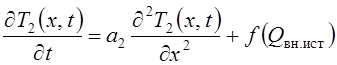 .
.
Суть внутренних источников тепла состоит в выделении скрытой теплоты кристаллизации в интервале температур между ликвидусом и солидусом. Если привести эту функцию к одинаковой размерности (град/с), то дифференциальное уравнение теплопроводности становится:
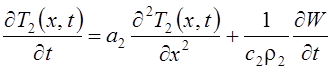 , где W – удельная объемная теплота
кристаллизации сплава; с2 – удельная теплоемкость сплава в
интервале кристаллизации; r2
– плотность сплава в интервале кристаллизации.
, где W – удельная объемная теплота
кристаллизации сплава; с2 – удельная теплоемкость сплава в
интервале кристаллизации; r2
– плотность сплава в интервале кристаллизации.
Полученное уравнение теплопроводности является неоднородным и для решения его в системе с другими дифференциальными уравнениями Фурье необходимо привести это уравнение к однородному.
Это можно сделать, если коэффициент температуропроводности а2
представить в виде некоторого эффективного значения, в котором будет учтено выделение
скрытой теплоты кристаллизации – 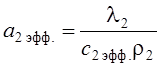 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.