Оптимизация технологических процессов производства электронной аппаратуры: Методические указания к лабораторным работам по дисциплине "Технология электронной аппаратуры", страница 8

где     - дисперсия в υ - точке;j - порядковый номер параллельного опыта в данной точке плана матрицы;  - среднее арифметическое значение показателя оптимизации в параллельных опытах в точке;  - значение параметра оптимизации в - точке; m-1 - число параллельных наблюдений в точках плана матрицы.

Для проверки гипотезы однородности дисперсии следует пользоваться критерием Кохрена, который основан на законе распределения отношения минимальной дисперсии к сумме всех дисперсий, т.е.

                                                                                                                     (3.7)

где     G- критерий Кохрена;  - максимальная дисперсия в υ-й точке.

Далее проверяют гипотезу в воспроизводимости измерений, заключающуюся в определении того факта, при котором выборочная дисперсия для каждой точки плана матрицы однородны.

Для этого следует задать уровень значимости g=5%, определить число степеней свободы V₁=m-1 и V₂=M, найти табличные значения критерия Кохрена G_кр при соответствующих степенях свободы. Если расчетное значение G, определенное по формуле (3.7) окажется меньше найденного, то гипотеза об однородности дисперсий и воспроизводимости результатов принимается. Если проверка дала отрицательный результат, то следует увеличить число параллельных опытов [5].

Далее следует выбирать уровень значимости по всем критериям (Кохрена, Стьюдента, Фишера), одинаковыми при решении поставленной задачи.

Если дисперсии однородны, то их следует усреднить, т.е. найти дисперсию параметра оптимизации по формуле

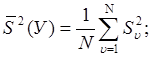                                                                                                                     (3.8)

где  - средняя арифметическая дисперсия всех различных точек плана матрицы или дисперсия параметра оптимизации; N - общее число различных точек в плане матрицы планирования.

3.4. Построение математической модели процесса групповой пайки

Как указывалось выше, пользуясь методом планирования эксперимента, можно получить описание изучаемого процесса в виде

где выборочные коэффициенты параметров модели процесса , и т.д. являются лишь оценками для теоретических коэффициентов , и т.д., а  - оценка математического ожидания показателя параметра оптимизации процесса.

Коэффициент регрессии определяют умножением данных  на данные , в кодовых обозначениях с последующим делением полученного произведения на общее число точек в плане матрицы, т.е. по формуле:

                                                                                                                     (3.9)

где      - коэффициенты регрессии 0,1,2,,...K;  - номер (фактора в кодовых обозначениях) столбца в плане матрицы 0,1,2,...K;  - среднее арифметическое по m опытов в точке с номером υ.

После нахождения коэффициента находится дисперсия ошибки определения коэффициентов.

При равном числе параллельных опытов (m-1), во всех точках плана матрицы дисперсию ошибки определения коэффициента регрессии определяем по формуле

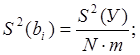                                                                                                                   (3.10)

где      - дисперсия ошибки определения коэффициента,  - дисперсия показателя параметра оптимизации. Значение  для всех коэффициентов одинаковое.

Среднеквадратическое отклонение дисперсии ошибки определения коэффициента регрессии  определяется по формуле:

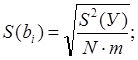                                                                                                                   (3.11)

Значение  для всех коэффициентов одинаковы. Значимость коэффициентов регрессии определяют по t- критерию Стьюдента. Для каждого коэффициента вычисляют значения t_i - критерия по формуле:

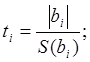                                                                                                                   (3.12)