Регулировка в зависимости от метода подбора компенсирующих элементов может быть дискретной и непрерывной. Дискретная регулировка используется в тех случаях, когда требует компенсировать вполне определенные значения выходного параметра и когда связь выходного параметра и параметра регулировочного элемента определена. Непрерывная регулировка предполагает возможность задать уровни выходного параметра через малые значения параметра регулировочного элемента, определяемые чувствительностью измерительной аппаратуры.
В зависимости от способа организации регулировки используются два метода:
- метод регулировки по измерительным приборам (инструментальная регулировка);
- метод регулировки путем сравнивания с образцом (метод копирования) [11].
В общем случае математическая постановка задачи регулировки объекта по диапазону независимой переменной ti (частоты, времени, напряжения и т.д.) выглядит следующим образом [11,12].
Допустим, что выходной параметр U(ti) регулируемого объекта отличается от требуемого на величину DU(ti). Изменение параметров регулировочных элементов DPi вызывает изменение выходного параметра на DUp(ti). Тогда значение регулировки состоит в выборе параметров регулировочных элементов так, чтобы выполнялось соотношение:
![]() (6.1)
(6.1)
Исходя из [11] математическую модель можно получить, разложив соотношение (6.1) в ряд Тейлора и ограничиваясь в виду малости отношений параметров только первыми членами ряда:
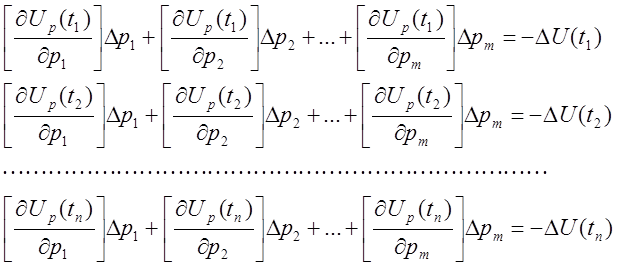 (6.2)
(6.2)
Поиски решения системы (6.2) осуществляется во время регулировки ЭА. Частные производные могут быть определены заранее аналитически и экспериментально.
Наиболее распространенным является способ регулировки путем последовательного подбора (классический метод) [12]. По этому методу регулировку начинают в первой точке t1, и первым регулировочным элементом p1, доводят выражение (6.1) до нуля, затем во второй точке погрешность доводят до нуля вторым элементом и т.д. до n-ой точки. Далее процесс повторяется несколько раз, пока в ходе последовательных приближений погрешность системы во всех заданных точках не обратится в нуль.
Другой способ регулировки позволяет систему уравнений (6.2) решить при помощи определителей:
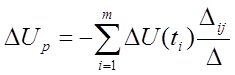 , (6.3)
, (6.3)
где D - главный определитель системы уравнений (6.2); Dij – соответствующий минор.
В этом случае процесс регулировки производится в следующем порядке:
а) в заданных точках определяются параметры DU(ti);
б) по рассчитанным коэффициентам
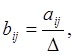 (6.4)
(6.4)
где 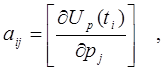 (6.5)
(6.5)
вычисляются изменения выходной величины DU(ti) в результате введения параметра Drj
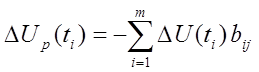 (6.6)
(6.6)
в) устанавливают систему в выбранные положения, изменяя Drj , чтобы на выходе выполнялось соотношение (6.1).
Следующий способ регулирования, обеспечивающий минимальное среднеквадратическое отклонение системы от нуля, требует выполнения условия
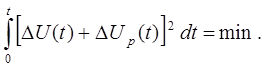 (6.7)
(6.7)
Искомые величины определяются по формуле:
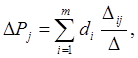 (6.8)
(6.8)
где
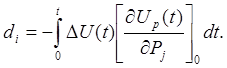 (6.9)
(6.9)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.