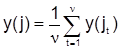Другие предметы \ Методология планирования и проведения современного эксперимента

Сборник лабораторных работ по курсу "Методология планирования и проведения современного эксперимента". Часть 2. Ортогональные и рототабельные центральные композиционные планы, страница 6

.                                                  (2.4)

При этом при проведении эксперимента с реальным объектом опыты в одной точке факторного пространства проводят не подряд, а обходят все точки пространства в первой серии опытов, затем во второй, … в ν-й. Для уменьшения влияния внешней среды и неконтролируемых факторов внутри каждой серии точки факторного пространства обходят случайным образом – рандомизируют последовательность опытов. Рандомизацию опытов можно провести с помощью генератора случайных чисел. При формировании задания для выполнения лабораторной работы рандомизация производится ЭВМ автоматически.

     2.3. Проверка воспроизводимости опытов (однородности дисперсий)     

Опыт считается статистически воспроизводимым, если дисперсия σy2 параметра y однородна (одинакова в каждой точке) факторного пространства. Оценка дисперсии определяется для каждой j-й точки факторного пространства по соотношению:

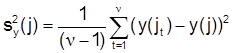.                                  (2.5)   

Гипотезу об однородности дисперсий проверяют с помощью критерия Кохрена. Расчетное значение этого критерия вычисляют по формуле:

,                                                   (2.6) а его критическое значение Gкр находят из таблиц распределения Кохрена по числу степеней свободы числителя q1 = ν – 1 и знаменателя q2 = N и уровню значимости α (см. приложение 1). Если Gр < Gкр гипотеза об однородности принимается, в противном случае – отвергается и тогда эксперимент необходимо повторить, изменив условия его проведения (набор факторов, интервал их варьирования, точность измерительных приборов и пр.). Например, если при варьировании какого-то фактора изменение исследуемого параметра сравнимо с погрешностью эксперимента, то интервал варьирования необходимо увеличить примерно на порядок.

      2.4. Расчет оценок и проверка значимости коэффициентов регрессионного                                                                                                             уравнения     

Информационная матрица М ортогонального ЦКП имеет вид

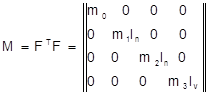,                                              (2.7)

где m0 = N = 2n-p + 2n + 1;  m1 = 2n-p + 2α2;

m2 = 2n-p(1-β2) + 2(α2- β2) + (2n-1)β2; m3 = 2n-p;

In – единичная матрица размером n х n; v – число сочетаний из n по 2.

Соответственно дисперсионная матрица

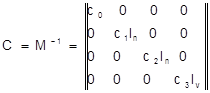,                                              (2.8)

где . Значения сi  для некоторых n приведены в табл 2.2.

Тогда соотношения для расчета оценок регрессионных коэффициентов имеют вид

                  (2.9) где - значение зависимой переменной y в j-й точке плана при t-м параллельном опыте.

Оценки диперсий коэффициентов регрессии определяются выражениями:

                                                       (2.10) где s2 – дисперсия ошибок наблюдений;

Гипотеза о статистической значимости (отличии от нуля) коэффициентов регрессии проверяется критерием Стьюдента.

                                  (2.11)

Критическое значение критерия tкр находят из таблицы распределения Стьюдента по числу степеней свободы и уровню значимости α (см. приложение 2).

Если неравенство выполняется, то гипотеза о значимости коэффициента принимается, а противном случае коэффициент считается незначимым и приравнивается к нулю.

Так как все коэффициенты оцениваются независимо, то изменение оценки любого коэффициента (например, исключение соответствующего члена из уравнения) не приводит к изменению других оценок и их дисперсий. Исключение составляет коэффициент b0, т.к. он связан с оценками при квадратах переменных, поэтому исключение квадратичных членов приводит к изменению b0.

Необходимо помнить, что незначимость коэффициента может быть обусловлена и неверным выбором интервала варьирования фактора. Поэтому иногда бывает полезным расширить интервал варьирования фактора и провести новый эксперимент.      

     2.5. Проверка адекватности полученной ММ

Адекватность ММ проверяется по F – критерию Фишера. Его расчетное значение определяется соотношением (1.14)

Скачать файл