Сборник лабораторных работ по курсу "Методология планирования и проведения современного эксперимента". Часть 2. Ортогональные и рототабельные центральные композиционные планы, страница 2

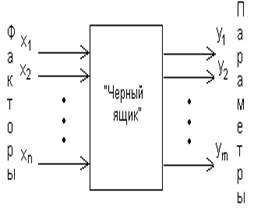
При планировании эксперимента исследуемый объект представляется “черным ящиком” (рис. 1.1), на который воздействуют факторы x_i. Каждый фактор x_i может принимать различные значения, которые называют уровнями фактора, а множество возможных                       уровней – областью определения G_i фактора x_i. Эта область может быть непрерывной и дискретной, ограниченной и неограниченной.

Рис. 1.1.

При выборе факторов необходимо учитывать требования к их совместимости и независимости. Совместимость предполагает допустимость любой комбинации факторов, а независимость – отсутствие между факторами корреляционной связи (это требование не всегда удается полностью выполнить, но сильная корреляционная связь недопустима).

К исследуемым параметрам (функции отклика) также предъявляется ряд требований. Они должны быть:

-  эффективными, то есть способствовать скорейшему достижению цели;

-  универсальными (быть характерными не только для исследуемого объекта);

-  статистически однородными, то есть по определенному набору факторов x_i с точностью до погрешности эксперимента должно соответствовать определенное значение параметра y_j.    

Кроме того, параметры должны выражаться количественно одним числом, иметь физический смысл и существовать при любом состоянии объекта.

Геометрический аналог параметра называют поверхностью отклика, а пространство, в котором строят эту поверхность – факторным пространством. Размерность факторного пространства равна числу воздействующих факторов. Так, например,  если их два, то это факторная плоскость.

При планировании эксперимента требуемых свойств ММ добиваются выбирая условия проведения опытов. Множество точек факторного пространства, в которых проводится эксперимент, представляется с помощью плана эксперимента

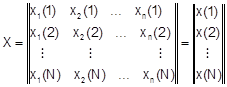
где n – число факторов; N – число точек факторного пространства. Точка 

называется центром плана.  Если центр плана совпадает с началом координат, то план называется центральным. Если на исследуемый объект действует много факторов, механизм которых неизвестен, то для построения ММ объекта используют, как правило, алгебраические полиномы, называемые уравнениями регрессии. Полиномами можно описать любую аналитическую функцию как угодно точно. Однако с ростом степени полинома резко возрастает число оцениваемых параметров, поэтому обычно ограничиваются второй степенью. Например, для двух факторов x₁ и x₂:

полином 0-й степени y = b₀;

полином 1-й степени (линейная модель)

                                             (1.1)

полином 2-й степени (квадратичная модель)

                                 (1.2)

В общем виде можно записать

, где: b = (b₀, b₁,…,b_k)^T  - вектор неизвестных параметров ММ, оценки которых требуется найти путем обработки экспериментальных данных;

-вектор известных функций, выбранных для ММ, например, для (1.1)  вектор , для (1.2) - .

Пусть результаты эксперимента, проведенного в N точках x(1), x(2),…,x(N) с координатами , представлены вектором наблюдений . Причем в каждой точке x(j) факторного пространства может быть поставлено ν параллельных опытов, результаты которых будут y(j₁), y(j₂),…,y(j_ν). Тогда в качестве y(j) будем использовать среднее значение наблюдений в точке x(j)

                                        (1.3)

Оценки  неизвестных коэффициентов ММ, рассчитываются из уравнения , где

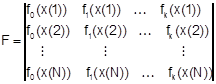                                        (1.4)  

К оценкам  обычно предъявляются требования несмещенности и минимальности дисперсии . Возможны и другие критерии для понятия “наилучшая оценка”, но приведенные выше два требования, приводящие при нормальном распределении результатов наблюдений к методу наименьших квадратов (МНК), позволяют провести статистический анализ полученных оценок и проверить адекватность ММ. Заметим также, что при МНК считается, что

-  результаты эксперимента не содержат систематических погрешностей;