Сборник лабораторных работ по курсу "Методология планирования и проведения современного эксперимента". Часть 2. Ортогональные и рототабельные центральные композиционные планы, страница 11

q_н = (2^n-p+2n)(ν - 1) + vn₀ - 1  – число степеней свободы.

Оценка дисперсии неадекватности s_a² определяется выражением

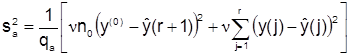,                        (3.6)

где  - число степеней свободы, w – число незначимых коэффициентов регрессии.

Если Fр<Fкр, то модель считается адекватной при выбранном уровне значимости 1-Р, где Р – доверительная вероятность.

3.3. Переход к физическим переменным

Для записи ММ в реальных физических величинах производят обратный переход от стандартизованного масштаба к натуральному. Это можно сделать, использовав соотношение (2.1). После чего записывают окончательный вид модели.

3.3.  Пример расчета рототабельного ЦКП

Пусть требуется исследовать влияние производственных факторов (U - опорное напряжение (х₁), I - ток потребления (х₂), Т - конечная температура нагрева (Х₃)) на качество производства магнитных дисков. Номинальные значения факторов:   U_н=30 В, I_н =18 А, Т_н = 220 °С.

Составим рототабельный ЦКП для трех серий опытов при интервалах варьирования U - 3В, I - 2А, Т - 20°С. Для стандартизации масштабов факторов условия проведения опытов сведем табл. 3.3.

После составления МП эксперимента и проведения рандомизированных опытов запишем полученные результаты в табл. 3.4. где у(j) – количественный параметр, характеризующий качество обработанной поверхности магнитных дисков.

Табл. 3.3

Условия проведения РЦКП

Характеристика плана	Стандартный масштаб xi	Натуральный масштаб
		X1=U, B	X2=I, A	X3=T, 0C
Нулевой уровень Верхний уровень Нижний уровень Звездные точки	0 +1 -1 +1,682 -1,682	30 33 27 35,046 24,954	18 20 16 21,364 14,636	220 240 200 253,64 186,36

Проведем статистическую обработку полученных результатов. Для проверки воспроизводимости опытов по критерию Кохрена (2.6) при выбранном уровне значимости α=0,05  вычислим в каждой точке факторного пространства среднее значение (2.4) и оценку дисперсии наблюдений (2.5) исследуемого параметра. Рассчитаем оценки коэффициентов регрессионного уравнения и их дисперсий по соотношениям (3.2) и (3.3). По критерию Стьюдента (3.4) определим статистическую значимость коэффициентов регрессии при α=0,1. Результаты сведем в табл. 3.5. Так как коэффициент b₃₃ оказался статистически незначимым, он должен быть исключен из ММ. Это в свою очередь может привести к изменению оценок дисперсий всех коэффициентов, а также оценок коэффициентов ,  и . Для расчета новых оценок коэффициентов воспользуемся общим соотношением (1.6), где матрица

Дисперсии оценок коэффициентов найдем (1.7) из ковариационной матрицы .

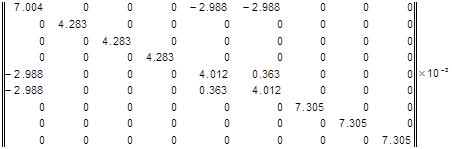
Полученные результаты сведем в табл. 3.6. Проверка по критерию Стьюдента показывает, что на этот раз незначимых коэффициентов нет. Таким образом, искомая математическая модель в нормированных координатах получена. Проверим ее адекватность по критерию Фишера (1.14) при α=0,05. Для этого найдем оценки дисперсий наблюдений и неадекватности по соотношениям (3.5) и (3.6) соответственно. Так как Fр = 1,51 < Fкр = 2,32, то модель считаем адекватной при уровне значимости 5 %. После перехода к физическим переменным получаем ММ:

3.6 порядок выполнения работы

1.  В соответствии с индивидуальным заданием необходимо перейти к стандартизованному масштабу факторов, составить матрицу рототабельного ЦКП и проверить ее свойства.

2.  Провести эксперимент (или имитацию эксперимента на ЭВМ).

3.  Проверить воспроизводимость опытов. Если дисперсии неоднородны повторить эксперимент.

4.  Рассчитать оценки коэффициентов регрессионного уравнения.

Табл 3.4.

Пример расчета рототабельного ЦКП