Сборник лабораторных работ по курсу "Методология планирования и проведения современного эксперимента". Часть 2. Ортогональные и рототабельные центральные композиционные планы, страница 3

-  результат в точке x(i) не зависит от результата в точке x(j);    

-  дисперсия результатов (дисперсия наблюдений) во всех точках эксперимента одинакова.

В случае невырожденности матрицы F^TF сумма

                               (1.5)

имеет единственный  минимум (единственное решение) при

,                                                   (1.6)

где матрица C = (F^TF)^-1, имеющая размерность (k+1) x (k+1), называется дисперсионной матрицей , а матрица M = (F^TF) – информационной матрицей.

Оценки , рассчитанные в соответствии с (1.6), отличаются от истинных коэффициентов тем больше, чем больше погрешность наблюдений. Показателями точности  и  являются их дисперсии σ_i² и σ_y² соответственно.  Эти дисперсии зависят не только от дисперсии погрешности наблюдений  σ², но и от выбора структуры ММ и точек постановки опытов в факторном пространстве. При этом в силу симметричности матрицы М для ковариационной матрицы  получаем

,                                                         (1.7)

откуда дисперсия σ_i² оценки коэффициента b_i

,                                                 (1.8)

а коэффициент корреляции между оценками b_i и b_t

 ,                                                  (1.9)

где c_ii и с_tt соответстыующие элементы ковариационной матрицы .

Таким образом, при известной дисперсии наблюдений σ² и предположении о нормальности закона распределения результатов наблюдений, можно построить доверительный интервал для заданной вероятности P(ε)

                                               , где                                           ,   Ф – функция Лапласа.

Дисперсию σ_y²  можно посчитать по формуле

                                              (1.10)

Если дисперсия σ² ошибок наблюдений не известна, ее можно оценить по экспериментальным данным, в частности, по остаточной сумме квадратов   

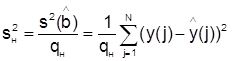                          ,                            (1.11)

где q_н = N – k –1 – число степеней свободы; - оценка значения исследуемого параметра в j-ой точке факторного пространства, полученные по ММ.

Если же в каждой точке факторного пространства проводится ν опытов, дисперсию ошибок наблюдения лучше оценивать с помощью суммы квадратов ошибок

,                               (1.12)

где q_н = N( ν – 1) – число степеней свободы.

Величина 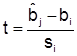 подчиняется t – распределению Стьюдента с q_н степенями свободы. Тогда для истинного значения i – ого коэффициента с вероятностью P получаем доверительный интервал , где t_kp соответствует выбранной доверительной вероятности  P и числу степеней свободы q_н. Заметим, что в общем случае оценка  и ее дисперсия зависят от оценок других коэффициентов и, если какой-то коэффициент исключается из ММ (например, в силу статистической незначимости), то оценки остальных коэффициентов и их дисперсии нужно пересчитать. При этом могут измениться как доверительные интервалы для , так и выводы относительно их значимости.

После расчета оценок коэффициентов необходимо проверить адекватность полученной ММ. Делают это сравнительная погрешность ММ с величиной, характеризующей погрешность наблюдений. Погрешность единичного наблюдения лучше оценить сравнением результатов нескольких параллельных опытов (1.12). Дисперсию, характеризующую неадекватность ММ, можно оценить по формуле

,                                  (1.13)

где q_a = N – k –1 - число степеней свободы.

Гипотеза об адекватности ММ проверяется с помощью F–критерия Фишера. Расчетное значение этого критерия представляет собой частное от деления оценки дисперсии неадекватности на оценку дисперсии единичного наблюдения

 ,                                                          (1.14)

а критическое значение F_кр находят по F-распределению (соответствующим таблицам) с числами степеней свободы q_a и  q_н соответственно и заданному уровню   доверительной вероятности P. Обычно выбирают P=0,95 или 0,99. Например, при q_a = 1, q_н = 4 и P = 0,99 находим, что F_кр = 21,2.