Сборник лабораторных работ по курсу "Методология планирования и проведения современного эксперимента". Часть 2. Ортогональные и рототабельные центральные композиционные планы, страница 10

Табл. 3.1

Рототабельный ЦКП

Табл. 3.2.

Параметры рототабельных ЦКП

Информационная матрица М рототабельного ЦКП близка к диагональной

, где L_n – вектор – столбец размерности n все элементы которого единичные; I_v – единичная матрица размером v x v; v – число сочетаний из n по 2;

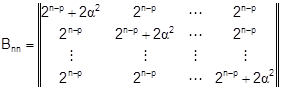
Оценки коэффициентов можно рассчитать, используя следующие соотношения

                         (3.2)

где x_i(j) – значение переменной x_i в точке j факторного плана;

Для оценки дисперсий оценок коэффициентов регрессии можно использовать соотношения:

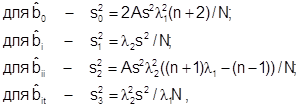                                               (3.3)

где  - оценка дисперсии наблюдений, s_н² определяется соотношением (3.5).

При оценке статистической значимости коэффициентов регрессии по критерию Стьюдента необходимо учесть, что условие значимости имеет вид

                          (3.4)

Необходимо помнить, что при рототабельном ЦКП оценки коэффициентов при линейных членах и парных взаимодействиях некоррелированы с оценками остальных коэффициентов, а при квадратичных членах – коррелированны между собой и оценкой свободного члена. Т.е. вывод о статистической значимости коэффициентов при линейных членах и взаимодействиях можно сделать независимо от значений остальных коэффициентов. Исключение любого из квадратичных членов приводит к изменению оценок остальных, а также оценки свободного члена b₀.

Адекватность ММ проверяется по F-критерию Фишера. Его расчетное значение определяется соотношением (1.14)

Если эксперимент повторяется  ν раз в каждой точке плана, то оценку дисперсии ошибок наблюдений s_н² можно найти по формуле

                  (3.5)

где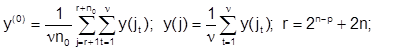

y(j_t) – значение зависимой переменной в j-й точке плана при i-м параллельном опыте;