





















Источники неопределённостей
Одним из основных требований к работе автоматических систем является высокая точность или высокие требования к обеспечению качества выходных процессов. При этом полагается решаемой задача устойчивости.
Расчёт управляющих устройств классическими методами обеспечивает требуемую точность, если модель объекта управления и условие функционирования системы абсолютно известны. Основные источники неопределённостей следующие неопределённость математической модели ОУ, неопределённость характеристик среды функционирования системы, неопределённость целевого условия (неопределенность цели фунуционирования).
Неопределенность мат. модели порождается линеаризацией нелинейных уравнений динамической сис-мы, а также параметрической неопределенностью.
Отметим, что регулятор, обеспечивающий устойчивость системы, может обеспечить заданную точность только при ограниченном диапазоне вариаций характеристик ОУ и условий его функционирования.
Виды неопределённостей
Параметрическая неопределённость. - зависимость свойств ОУ от неизвестных параметров. Параметры могут быть неизвестными и переменными. Темп их изменения сравним с темпом процессов в объекте управления или темпом изменения внешних воздействий. Параметрическая неопределённость может быть априорной или текущей. Динамические системы с таким видом параметрической неопределённости называются нестационарными.
Неопределённость внешних условий Значительное влияние на поведение реальных систем управления оказывает окружающая среда. Неопределённость внешних условий учитывается в математической модели в виде возмущающих воздействий и сигналов задания. В большинстве практических случаев точная форма (характер поведения) внешних воздействий остаётся неизвестным вплоть до начала работы системы управления.
Наряду с детерминированными задачами пространственного движения, в которых желаемая траектория задана заранее существуют плохо определённые задачи, в которых эталонная траектория задана неточно или её аналитическое описание априорно неизвестно, для формирования управления могут использоваться только текущие измерения отклонений от траектории. Т.е. целевой функционал может быть задан косвенно.
 Рассматриваемая задача соответствует движению некоторого кинематического
механизма вдоль «физически заданного» контура, выявляемого с помощью сенсоров,
и характеризуется неопределённостью цели. Рассмотренные виды
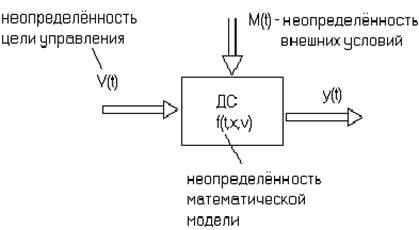
неопределённостей можно иллюстрировать следующим рисунком
Рассматриваемая задача соответствует движению некоторого кинематического
механизма вдоль «физически заданного» контура, выявляемого с помощью сенсоров,
и характеризуется неопределённостью цели. Рассмотренные виды
неопределённостей можно иллюстрировать следующим рисунком
ДС – динамическая система,
f(.) – математическая модель системы,
V (t) – вектор входных воздействий,
M (t) – вектор возмущающих воздействий,
y (t) – вектор выходных переменных.
Неопределённости математической модели и внешних условий учитываются как возмущения в описании динамических систем. Различают три основных вида возмущений: параметрические, аддитивные, структурные.
Номинальная система – математическая модель
динамической системы для идеальных условий при отсутствии возмущений ![]() и возмущённой системы
и возмущённой системы ![]() , где ∆(х, t) определяет вид возмущения.
, где ∆(х, t) определяет вид возмущения.
1. Если ½∆(x, t)½≤ C1½х½ и ∆(0,t) = 0, где C1= const, C1 > 0 , то возмущение называется мультипликативным или параметрическим.
Пример 1.3.
Пусть номинальная система линейная, f(x,
t)=A0x.
Возмущение возникло из-за отклонений параметров матрицы коэффициентов, А=А0+А1,
от номинальных значений. Возмущённая система имеет вид ![]()
т.е. ∆(x,t)=A1x. В этом случае С1=½А1½и ½∆(x,t)½£ ½А1½½х½.
2. Если для любого x и tвыполняются условия ½∆(x,t)½£ С2 и ½∆(0,t)½¹ 0, то такой вид вариаций математической модели называют аддитивными возмущениями (или постоянно действующими возмущениями, сигнальными).
Пример 1.4. Модель возмущённой системы имеет вид
![]() ½М(t)½£ С2
.
½М(t)½£ С2
.
3. Третий вид возмущений называется сингулярным (или структурным). Для его характеристики представим номинальную модель следующим уравнением
![]() (1.2)
(1.2)
где f0(x, t), g(x, t) – n-мерные вектор – функции, u(x, t) – скалярная функция управляющего воздействия. Структурные возмущения возникают вследствие так называемой, «паразитной динамики», пример, неучтенные малые инерционности в объектах управления. Возмущенная модель может быть определена в виде
![]() (1.3)
(1.3)
![]() zÎRm
(1.4)
zÎRm
(1.4)
гдеD,N,c – матрица и векторы постоянных коэффициентов соответствующих размерностей. m - малый постоянный параметр, z – вектор состояния модели. Уравнение (1.4) описывает «паразитную динамику». Пусть справедливо выражение
![]() ;
; ![]() ,
, ![]()
![]() - характеристический
полином,
- характеристический
полином,
![]() , тогда
, тогда ![]() - гурвицев полином.
- гурвицев полином.
![]() ;
; ![]() ,
, ![]()
Тогда при m= 0 имеем ![]() , т.е.
, т.е. ![]() .
.
Если m обращается в ноль, то изменяется структура системы (1.3),(1.4)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.