Виды и источники неопределенностей. Виды возмущений. Основные классы адаптивных систем. Отличие поисковых и беспоисковых систем с самонастройкой. Особенности прямого и непрямого адаптивных подходов, страница 8

НЕПРЕРЫВНЫХ АДАПТИВНЫХ  СИСТЕМ С ЭТАЛОННЫМИ МОДЕЛЯМИ

14)     Градиентный алгоритм, последовательность синтеза адаптивной системы.

Градиентный алгоритм относится к базовым алгоритмам адаптации. Вектор градиента всегда направлен в сторону максимального локального роста функции. Значит, если вектор скорости настраиваемых параметров () направить в сторону антиградиента , то реализуется последовательный спуск в локальный минимум. Если 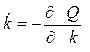 , тогда Q будет убывать.

Этапы синтеза адаптивной системы

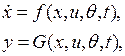 (2.1)    (2.5)          (2.6)

Адаптивная система (2.1), (2.5), (2.6) имеет двухуровневую схему, поэтому выделяют два основных этапа расчета:

3)  синтез основного контура (2.5),

4)  синтез контура адоптации (2.6).

К методам синтеза основного контура, получившим наибольшее распространение, относятся:

1)  метод этал. уравн (или метод инвариантности). Уравнение закона управления получается из равенства правых частей уравнений эталонной модели и модели объекта управления;

2)  метод модального управления. Закон управления определяется, исходя из желаемых показателей качества переходного процесса;

3)  методы оптимального управления. Закон управления получается в результате решения задачи оптимизации по управл воздействию некоторого обобщённого показателя качества;

4)  метод сингулярных возмущений. Для синтеза закона управления используется упрощённая модель системы, которая получается в результате выделения подсистем быстрых и медленных процессов. Закон управления определяется по модели, описывающей подсистему медленных движений.

В результате применения одного из перечисленных методов получают «идеальный» закон управления. Как правило, вид уравнения основного контура следующий

где k_х,, k_r – матрицы коэффициентов соответствующих размерностей.

Второй этап синтеза сводится к определению оператора k_t (2.6). Алгоритм настройки коэффициентов регулятора может быть определен

8)  вторым методом Ляпунова. Алгоритм адаптации получается из условия устойчивости замкнутой системы. Функция Ляпунова обычно выбирается в виде суммы целевого функционала и квадратичной формы от рассогласования между настраиваемыми и идеальными параметрами.

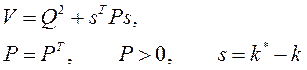
k^* - идеальные значения параметров,  k- настраиваемые коэффициенты;

9)  градиентным методом. Алгоритм адаптации строится в направлении антиградиента целевой функции по рассогласованию или настраиваемым коэффициентам. Алгоритм настройки коэффициентов зависит от функции чувствительности, в которую входят неизвестные параметры объекта управления. Поэтому используют приближенные методы вычисления функции чувствительности;

10)  методом скоростного градиента. Изменение коэффициентов осуществляется в направлении антиградиента производной целевой функции по настраиваемым коэффициентам. В результате не требуется определения функции чувствительности;

11)  методами, основанными на теории гиперустойчивости. Синтез алгоритма адаптации осуществляется из условия гиперустойчивости замкнутой системы;

12) методами, основанными на организации скользящих режимов;

13) методом мажорирующих функций и т.д.

15)     Определение и формы алгоритма скоростного градиента.

Общая характеристика схемы скоростного градиента

Суть метода скоростного градиента заключается в следующем: настройка параметров осуществляется в направлении, противоположном скорости изменения целевого функционала вдоль траектории обобщенного настраиваемого объекта.

Алгоритмом скоростного градиента принято называть правило изменения вектора настраиваемых коэффициентов (q), задаваемое  уравнением вида

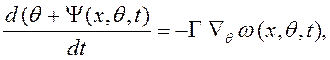                                        (3.22)

где Ñ- дифференциальный оператор, Г = Г ^Т > 0 – квадратная матрица коэффициентов передачи,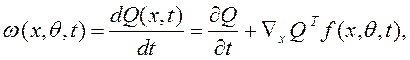      

здесь Q(.) – целевой функционал, f (x,q, t) – вектор-функция, описывающая ОНО,

y(.) – вектор-функция, удовлетворяющая условию псевдоградиентности:

Это условие эквивалентно требованию, чтобы условие псевдоградиентности -  угол j между векторами y и w лежал в пределах от - 90⁰ до + 90⁰ (рисунок 3.5) -  выполняется, если            или