Виды и источники неопределенностей. Виды возмущений. Основные классы адаптивных систем. Отличие поисковых и беспоисковых систем с самонастройкой. Особенности прямого и непрямого адаптивных подходов, страница 11

Согласно (4.21)  элементы  вектор-функции  имеют следующий вид:

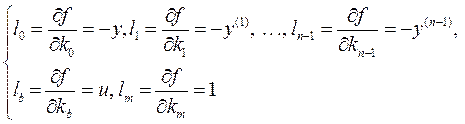Для реализации закона управления (4.22) требуется информация о производных выходной переменной, оценку которых можно получить с помощью дифференцирующих фильтров.  Дифференциальное уравнение ФОП имеет вид:

Порядок адаптивной системы  равен  где - порядок адаптивного регулятора,  ,  его значение  зависит от количества неизвестных параметров и присутствия внешнего возмущения в  объекте управления.

19)     Последовательность синтеза адаптивных систем пониженного порядка,  системы с сигнальной адаптацией.

Модель линейного одноканального нестационарного объекта управления n-го порядка описывается уравнениями вида: 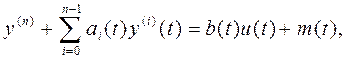   (4.9) 

Разложим параметрические  возмущения  в ряд Тейлора с целью выделения постоянной и переменной составляющей по формуле:

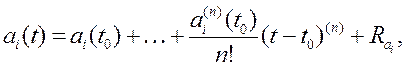
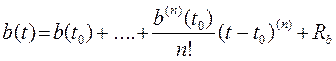  (4.11)

Выделим в (4.11) первые члены разложения:  причем   Получим модифицированную модель объекта: 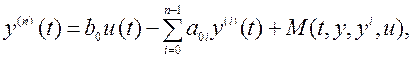                                (4.13) где 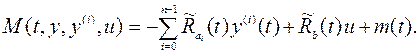  здесь , причем  равны либо расчетным номинальным значениям, либо априори известным верхним оценкам соответствующих коэффициентов. Используя  требования к показателям качества замкнутой системы, формируем желаемое диф-ное уравнение, того же порядка что порядок уравнения объекта. Разрешаем относительно старшей производной:   (4,14)

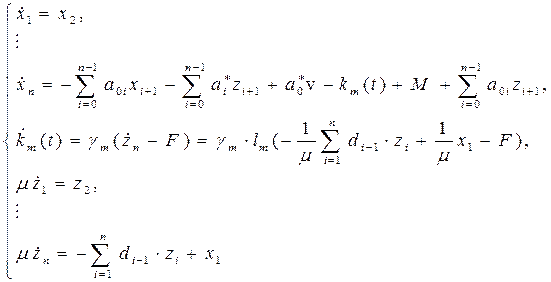Приравниваются правые части (4.13), (4.14), полученное уравнение разрешается отн-но управ. переменной, после чего выполняется замена неизвестных коэф-тов, также функции  соответ-ми коэф-ми регулятора: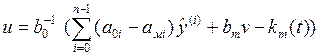 (4.24)    где k_m(t)  настраивается по алгоритму:   ,  (4.25)  где γ_m –коэф-т передачи адаптера, l_m – вспомогательная фун-я. С помощью γ_m и l_m достигается поставленная цель управления, т.е. значения γ_m и l_m  определяются из условия устойчивости адаптивной системы.  Оценка  n производных осуществляется с помощью диф.:   (2.37) В пространстве состояния система имеет вид:

Переменные состояния ФОП выберем следующим образом:

,

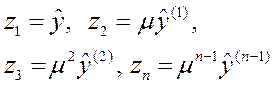Как видно из (4.26), порядок адаптивной системы с одним контуром адаптации равен  Нетрудно видеть, что система с сигнальной адаптацией (4.26) может быть также отнесена к классу робастных систем с астатическим регулятором (астатический регулятор со старшей производной)

20)     Системы пониженного порядка с сигнально-параметрической адаптацией синтезированные методом вектора скорости.

Модель линейного одноканального нестационарного объекта управления n-го порядка описывается уравнениями вида: 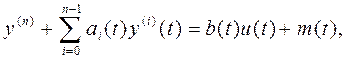   (1)  Разложим параметрические  возмущения  в ряд Тейлора с целью выделения постоянной и переменной составляющей.Учтем первые два члена ряда   и первые члены ряда разложения , . Согласно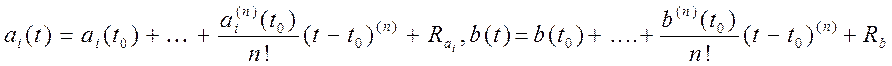 

Имеем   где  остаточный член. Примем  второй член ряда представляет собой линейную функцию времени:      Тогда уравнение объекта (1) примет вид:

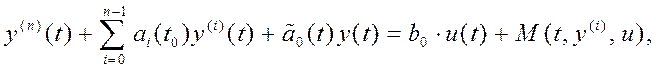  (2)           в которой неизвестная функция M(t) и неизвестный переменный параметр . Таким образом, на  объект действуют   параметрическое и аддитивное возмущения, поэтому метод адаптации будет сигнально-параметрическим. Используя  требования к показателям качества замкнутой системы, формируем желаемое диф-ное уравнение, того же порядка что порядок уравнения объекта. Разрешаем относительно старшей производной получаем описание эталонной модели:       (3)

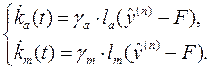Приравниваются правые части (2), (3), полученное уравнение разрешается отн-но управ. переменной, после чего выполняется замена неизвестных коэф-тов, также функции  соответ-ми коэф-ми регулятора: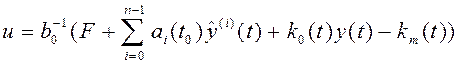   

изменение настраиваемых коэф-тов подчиняются алгоритмам:

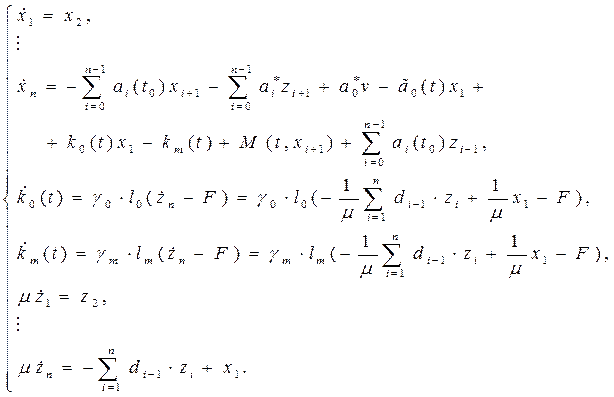  где γ_m, γ_a-коэффициенты передачи адаптера, l_{m ,} l_а  -  вспомогательная функция. Уравнения системы с сигнально-параметрической адаптацией, записанные в расширенном пространстве состояний  имеют вид:        

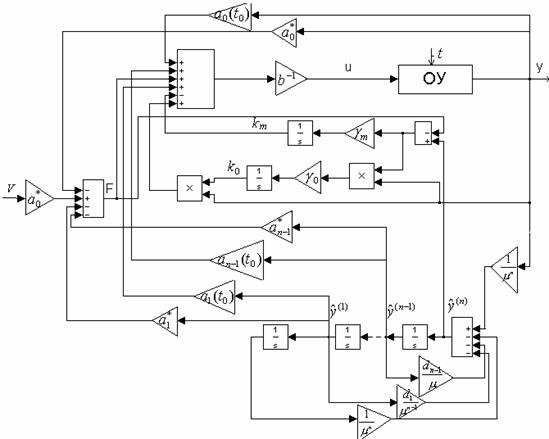Рисунок 4.11. Структурная схема адаптивной системы с двумя контурами адаптации

(В20  Системы пониженного порядка с сигнально-параметрической адаптацией синтезированные методом вектора скорости. )

Рисунок 4.10 Структурная схема адаптивной системы с одним контуром адаптации