Виды и источники неопределенностей. Виды возмущений. Основные классы адаптивных систем. Отличие поисковых и беспоисковых систем с самонастройкой. Особенности прямого и непрямого адаптивных подходов, страница 10

«Идеальный» закон управления (3.45) или (3.46) не реализуем, так как параметры ОУ не известны. Заменим идеал. коэф. регулятора () настраиваемыми (k^r, k^x). Структура регулятора описывается .  (3.50) Подставив  (3.50) в ОУ, получим уравнение обобщенного настраиваемого объекта (ОНО)       (3.51)

Синтез контура адаптации На этом этапе расчета системы определяются уравнения,  в соответствии с которыми настраиваются коэф-ты регулятора, т.е. алгоритмы изменения k^r, k^x .  Получим описание ОНО в отклонениях.

и подставим (3.50) в (3.43), тогда

         (3.52)

Введем расширенную матрицу отклонений настраиваемых коэф-тов от их «идеальных» значений  и вектор сенсоров, элементы которого измеряются или вычисляются на основе измерений 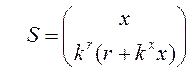         ,     dimS = px 1,   p = n + m.

Уравнение (3.52) примет вид  - уравнение системы в отклонениях.

Для исследования системы используем функцию Ляпунова вида

, (3.53)

где tr (.)– след матрицы (сумма элементов главной диагонали), .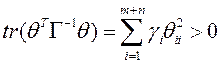

В силу уравнения (3.52) определим производную функцию V (3.53)

Вторая составляющая уравнения обращается в ноль, если  - алгоритм адаптации в отклонениях,     (3.54)    Производная исследуемой функции принимает видотрицательная определенность функции следует из гурвицевости матрицы коэффициентов эталонной модели. Матрица Н удовлетворяет уравнению Ляпунова:Полагая медленное изменение коэффициентов  и учитывая ранее введенные обозначения, получим вид алгоритмов адаптации:                           (3.55)

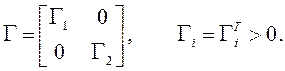
Замечание: 1. Для реализации рассмотренного адаптивного регулятора предполагаем введение в систему: - наблюдателя состояния;   - дополнительного динамического звена, формируемого желаемую траекторию системы. 2. Расчет системы проводится в предположении квазистационарности ОУ, поэтому адаптивная система не будет обладать свойством идентифицируемости (точного определения) параметров ОУ и будет обладать заданным качеством только при медленном темпе изменения параметрических возмущений. 3. В данном случае расчет проведен в системе с параметрической адаптацией, но изложенный подход позволяет определить алгоритм сигнально – параметрической адаптации.

Замечание:  Приведем промежуточные вычисления, поясняющие вид  уравнения (3.55),

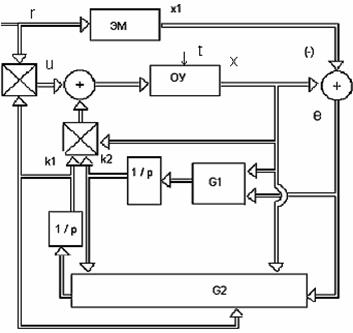
Структурная схема адаптивной системы (3.25), (3.26), (3.46), (3.55) изображена на рисунке 3.8 . Для обозначения элементов схемы приняты обозначения: .

Условия, при которых решена поставленная задача, являются условиями идентифицируемости  при  и, одновременно, условиями асимптотической устойчивости в целом

Замечание: Согласно описанию объекта коэффициент b₀точно не известен. Поэтому в адапторе можно использовать либо b_м, либо любое значение из заданного множества, которому принадлежит b₀ .

18)     Основные этапы синтеза адаптивных алгоритмов методом вектора скорости (синтез систем полного порядка).

Модель линейного одноканального нестационарного объекта управления n-го порядка описывается уравнениями вида: 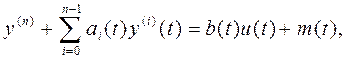   (4.9)  Цель функ-ния системы состоит в стабилизации с заданным качеством выходной переменной системы:   .  Уравнение основного контура можно получить методом эталонного уравнения. Полагаем, что желаемая динамика системы описывается  дифференциальным уравнением вида:   (4.17)

где – задающее входное воздействие. Уравнение (4.17) описывает эталонную модель. В процессе синтеза адаптивного регулятора полного порядка используем (4.9), разрешенное отн-но старшей производной 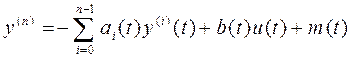         (4.18)

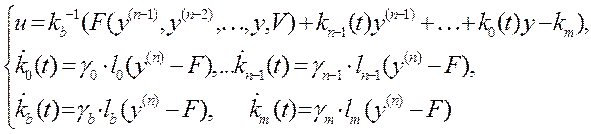Приравниваются правые части (4.17), (4.18), полученное уравнение разрешается отн-но управ. переменной, после чего выполняется замена неизвестных коэф-тов, также функции  соответ-ми коэф-ми регулятора:              (4.19) здесь - настраиваемые коэф-ты, i={0, 1,…,n-1}. Пусть коэф-ты регулятора образуют вектор , тогда алгоритм адаптации на основе метода вектора скорости:  (4.20А)  (4.20В)  где – матрица коэф-тов передачи, ; – вспомогательные вектор-функции. Для сходимости процессов в системе (4.9), (4.19), (4.20А)  элементы вектор-функции  определяются следующим образом:      (4.21)где 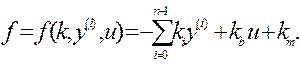 Таким образом, адаптивный регулятор описывается уравнениями: